Вимірювання швидкості руху молекул газу

· Швидкість руху молекул газу

· Дослід Штерна

Швидкість руху молекул газу. Прирівнюючи формули для середньої кінетичної енергії поступального руху молекул газу можна отримати вираз для середньої квадратичної швидкості руху молекул.

З формул і отримуємо .

Обчисливши за цією формулу середню квадратичну швидкість, наприклад, молекул азоту при t = 0 °С, отримуємо значення 500 м/с. Молекули водню при t = 0 °С мають швидкість 1800 м/с.

Коли вперше дістали ці числа (друга половина XIX ст.), то це приголомшило багатьох фізиків, і вони висловили сумніви щодо правильності молекулярно-кінетичної теорії. Адже відомо, що пахощі поширюються досить повільно: потрібні десятки секунд, щоб пахощі парфумів, розлитих в одному кутку кімнати, досяг іншого кутка. Наразі ви можете це легко пояснити великою кількістю зіткнень між молекулами.

Дослід Штерна. Вперше швидкість теплового руху атомів експериментально визначив у 1920 році німецький вчений-фізик О. Штерн (1888 - 1969). Він користувався приладом, схему якого зображено на мал. 24, а.

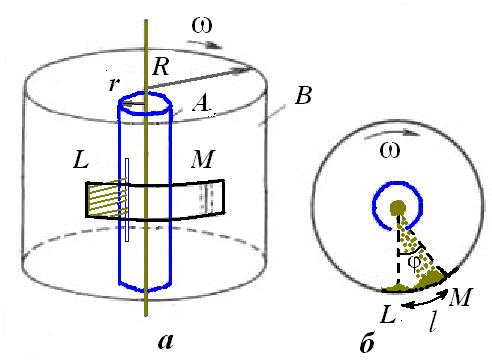
Мал. 24, а. Схема установки для вимірювання швидкості руху молекул; б – зміщення пучка атомів при обертанні циліндрів

Уздовж осі двох жорстко з’єднаних циліндрів (А і В) різних діаметрів зі спільною віссю розміщувався платиновий дріт, покритий шаром срібла. Внутрішній циліндр (А) мав щілину. Дріт нагрівався під час пропускання електричного струму через нього і при t = 1300 °С срібло з його поверхні випаровувалось. У такий спосіб у камері циліндрів, повітря з якої заздалегідь відкачувалося до тиску 1,3·10^-4 Па, утворювався газ із атомів Аргентуму. У результаті на зовнішньому циліндрі (В) навпроти щілини утворювався срібний наліт. Його положення на мал. 24, а, б визначається областю L.

Потім циліндри обертали із частотою ω. За час t, потрібний атомам для проходження відстані, що дорівнює різниці радіусів циліндрів (R – r), циліндри поверталися на деякий кут. Через це атоми, що рухалися зі сталою швидкістю, потрапляли на внутрішню поверхню великого циліндра (В) не проти щілини, а на певній відстані, у область М (мал. 24, а, б).

Зміщення нальоту пояснюється тим, що за час t, поки атоми срібла із швидкістю пролітають відстань (R – r), зовнішній циліндр встигає повернутись на кут . Відповідно, кожна точка поверхні зовнішнього циліндра зміщується на відстань , де - радіус зовнішнього циліндра, - лінійна швидкість руху точок на його поверхні. Це призводить до зміщення точок осідання атомів срібла.

Оскільки наліт в області М розмивається, то це підтверджує те, що не всі атоми мають однакову швидкість. Тому для подальших розрахунків використовують середнє значення швидкості .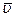

Таким чином час t, поки атоми срібла із швидкістю 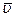пролітають відстань (R – r), можна визначити так: .

Звідки .

Знаючи радіуси циліндрів R та r, кутову швидкість їх обертання ω та вимірявши відстань () між областями L і М (між точками найбільшого скупчення атомів) можна визначити швидкість руху молекул.

У досліді О.Штерна було встановлено, що середня швидкість руху атомів срібла дорівнює 650 м/с.

Цей фундаментальний дослід є експериментальним доказом існування атомів речовини і правильності молекулярно-кінетичної теорії в цілому.

Дайте відповідь на запитання

1. Як можна визначити середню квадратичну швидкість руху молекул газу?

2. Побудуйте схему досліду Штерна і поясніть його сутність.

3. Запишіть формулу, за якою визначають середню швидкість руху атомів речовини в досліді Штерна.

4. Чому в досліді Штерна смужка срібла: а) зміщена; б) розмита по краях; в) неоднорідна за товщиною?

5. Подумайте, де залишиться слід атомів, швидкості руху яких більші від середньої швидкості, і як зміниться положення нальоту, якщо збільшити струм у дротині.