Операции над множествами

1) Пусть и произвольные множества. Множество С, состоящие из всех тех элементов, которые принадлежат хотя бы одному из множеств и , называется объединением множеств и и обозначается (рис.1). Таким образом,

.

Здесь и далее символы означают «по определению».

2) Множество С_, состоящие из всех тех и только тех элементов, которые принадлежат каждому из данных множеств и называется пересечением множеств и и обозначается , т.е.

(рис.2)

Рис.1 Рис.2

Пример. и , то по определению имеем

Операции объединения и пересечения обладают следующими свойствами:

1. коммутативности:

;

2. ассоциативности:

;

3. дистрибутивности:

;

4. идемпотентности:

,

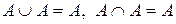Очевидно, что 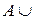Æ , Æ=Æ.

Если Æ, то будем говорить, что множества и не пересекаются.

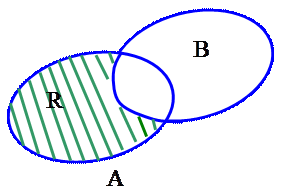
3) Разностью множеств и называется множество 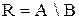, состоящее из всех элементов , которых нет в . Заметим, что в общем случае (рис.3.1). Но если 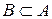, то

Рис. 3.1 Рис. 3.2

Пример. Если , то

4) Если 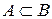, то разность называют дополнением множества А до множества и обозначают (или ). В тех случаях, когда рассматривается только подмножества некоторого основного множества , то дополнение множества до множества называют просто дополнением и пишут (или ).

Из этого определения следует, что

Æ, .

Свойства

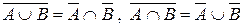
называют законами двойственности или законами де Моргана.

Множества, элементы которых являются числами, называются числовыми. Приведём основные примеры числовых множеств.

Множество натуральных чисел обозначается через , .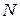

Во множестве 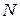действуют операции сложения и умножения.

Множество целых чисел обозначается через Z:

.

Во множестве 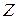действуют операции сложения, вычитания и умножения.

Множество рациональных чисел обозначается через ,

.

В множестве действуют все четыре арифметические операции. Множество всех действительных чисел – как рациональных, так и иррациональных, обозначается через . В нём выполняются все арифметические действия и извлекаются корни любой степени из неотрицательных чисел.

Эти множества являются подмножествами друг друга в следующем порядке:

.

1.1.2 Символика математической логики. Для сокращения записи в дальнейшем будем употреблять некоторые основные логические символы, или кванторы. Пусть a и b некоторые предложения.

1) Запись означает: “из a следует b ”, " Þ " символ импликации.

2) Запись означает “a и b эквивалентны”, т.е. что, из и из .

" Û "– символ эквивалентности.

Любую теорему в математике можно записать в виде или в виде , a – условия теоремы, а b – её утверждение.

3) Знак “"” означает: “каждый, любой, для каждого” и т. д. "– квантор общности. Например, 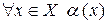означает: “для всякого элемента истинно утверждение ”.

4) Знак “$” означает “существует, найдется, имеется”. "$"– квантор существования. $ - перевернутая - начальная буква слова “Existenz” - “существует”. Например, означает: существует элемент такой, что для него истинно утверждение 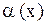. Если элемент хиз Х, для которого истинно утверждение , не только существует, но и единствен, то пишут: .

5) Знак “:” означает: “такой, что” или “такие, что”, специального названия он не имеет.

6) Знак “ ” или означает отрицание утверждения , " " - символ отрицания. Часто при доказательстве теорем используется метод "от противного", который использует равносильность предложений () и ().

7) Запись означает " и " (" " – символ конъюнкции).

8) Запись означает " или " (" " – символ дизъюнкции).

Отрезок, интервал, ограниченное множество. Введём следующие обозначения для подмножеств в .

Множество чисел х 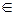, удовлетворяющих неравенствам 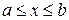, называется отрезком (с концами 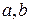) или сегментом и обозначается так:

, т.е. .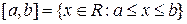

Множество чисел , удовлетворяющих неравенству , называется интервалом (с концами 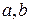) или открытом отрезком и обозначается так: (а, b ), т. е. (а, ) ={ : }.

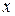
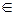
Множество чисел , удовлетворяющих неравенствам а или , обозначаются соответственно и называются полуоткрытыми отрезками или полуинтервалами. Первый, например, закрыт слева и открыт справа.

Отрезки, интервалы и полуинтервалы называются числовыми промежутками или просто промежутками.

Произвольный интервал (а, b ), содержащий точку мы будем называть окрестностью точки .

a x_{0 b}

Рис.4

В частности, интервал называют 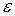- окрестностью точки

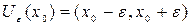
Пример. (10) =(9,9; 10,1).

Часто рассматривают множества, называемые бесконечными интервалами или полуинтервалами:

1) (), 2)( ], 3)(), 4)(), 5)[ ).

Первые их них есть множество всех действительных чисел (действительная прямая), остальные состоят их всех чисел, для которых соответственно:

2) , 3) , 4) , 5) .

Если и 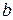конечны и , то число называется длиной сегмента или интервала , или полуинтервала (.

Пусть Х есть произвольное множество действительных чисел.

Говорят, что множество X ограничено сверху, если 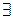(действительное), число М такое, что .

Ограничено снизу, если 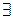число т такое, что .