 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Векторное произведение двух векторов и его приложения
|
|
Задача 8. Упростить выражение  .
.
Решение. Найдём векторные произведения для этого раскроем скобки, т.е. 

 .
.
Задача 9. Упростить выражение  , если
, если 
 .
.
 |

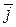
| Решение. Используя схему, получим, например, 
 , кроме того , кроме того  . .


|


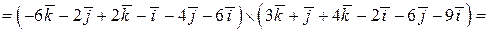





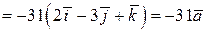 .
.
Задача 10. На материальную точку  действуют силы
действуют силы  ,
,  ,
,  . Определить величину и направляю-
. Определить величину и направляю-
щие косинусы момента равнодействующей сил относительно точки  .
.
Решение.  , где
, где 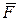
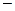 равнодействующая сил
равнодействующая сил  .
.
 ,
, 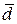
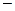 плечо, т.е.
плечо, т.е.
вектор  .
.
 .
.
 .
.
Направляющие косинусы момента есть координаты орта:
 .
.
Задача 11. Треугольник 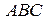 построен на векторах
построен на векторах  и
и  , где
, где  . Найти высоту, опущенную из вершины
. Найти высоту, опущенную из вершины 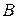 .
.
Решение.  . С другой стороны,
. С другой стороны,  , следовательно
, следовательно  . Найдём
. Найдём 


 .
.
 .
.
 .
.
4. Смешанное произведение трёх векторов и его приложения
Задача 12. Даны координаты вершин параллелепипеда 
 . Найти: 1) объём параллелепипеда; 2) высоту, опущенную из вершины C; 3) угол между вектором
. Найти: 1) объём параллелепипеда; 2) высоту, опущенную из вершины C; 3) угол между вектором  и гранью, в которой лежат векторы
и гранью, в которой лежат векторы 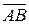 и
и 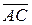 .
.
Решение. Определим векторы 
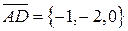 .
.

 1).
1).  .
.
2). 
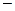 ?
?  ,
,  .
.

 . Тогда
. Тогда  .
.
| 3) Надо определить угол  .
Для этого определим угол между вектором .
Для этого определим угол между вектором  и вектором и вектором  , где , где  , т.е. , т.е.
|
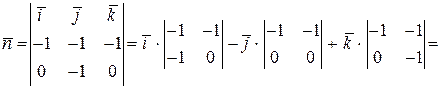
 .
.
Тогда  .
. 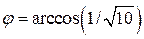 .
.
Угол  , т.е.
, т.е.  .
.
Задача 13. Проверить лежат ли четыре точки 
 в одной плоскости.
в одной плоскости.
Решение. Если точки лежат в одной плоскости, то и векторы, например,  лежат в одной плоскости, т.е. компланарны, следовательно, их смешанное произведение равно 0. Определим векторы:
лежат в одной плоскости, т.е. компланарны, следовательно, их смешанное произведение равно 0. Определим векторы:  ,
,  ,
,  .
.
 Составим определитель:
Составим определитель: 
Определитель равен нулю, следовательно, векторы линейно зависимы. Найдём линейную зависимость, например, вектора 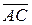 от
от 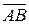 и
и  .
.  .
.

 . Тогда
. Тогда  .
.
Получим 

 . Тогда
. Тогда  .
.
Дата публикования: 2014-10-20; Прочитано: 843 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

