А л г о р и т м 1

Пусть игра Г определена 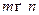матрицей и цена .

1. Отыскиваются седловые точки, они записываются в виде смешанных стратегий и включаются в формируемые подмножества крайних точек. В этом случае находится сразу и цена игры.

2. Проверяем, нет ли среди столбцов матрицы строго мажорирующих. Если столбец 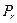– строго мажорирующий, то полагаем и 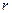-ый столбец матрицы вычеркиваем. Проверяем, нет ли среди строк матрицы строго минорирующих. Если строка является строго минорирующей, то полагаем , и -ую строку матрицы вычеркиваем (операции этого пункта не обязательны, но в случае удаления таких строк и столбцов можно сократить вычислительные трудности).

3. Выбираем квадратную подматрицу 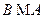порядка не меньше двух (множества номеров строк и столбцов, на пересечении которых стоит подматрица , будем обозначать символами , соответственно).

4. Вычисляется определитель матрицы . Если , то матрица отбраковывается и следует переход к п.3 алгоритма.

5. Вычисляется матрица , обратная для матрицы .

6. Вычисляется число , равное сумме всех элементов матрицы . Если , то матрица отбраковывается и следует переход к п.3 алгоритма.

7. Полагается . Согласно теореме 5.1 это число предполагается равным цене 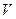. Если цена 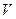игры к этому моменту уже известна и , то матрица отбраковывается и следует переход к п.3 алгоритма.

8. Находится решение системы уравнений , где вектор имеет размерность матрицы . Если среди координат решения имеется отрицательная, то матрица отбраковывается и следует переход к п.3 алгоритма.

9. Находится решение системы уравнений , Если среди координат решения имеется отрицательная, то матрица отбраковывается и следует переход к п.3 алгоритма.

10. Векторы 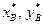расширяются (нулями) до 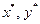на местах .

11. Проверяется выполнение неравенств

.

Если хотя бы одно из них не выполняется, то матрица отбраковывается и следует переход к п.3 алгоритма. Иначе переходим к п.12.

12. Векторы 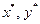включаются в формируемые подмножества крайних точек, число является ценой игры.

13. Если просмотрены не все квадратные подматрицы матрицы , то следует переход к пункту 3 алгоритма. Иначе следует переход к следующему пункту.

14. Выписываются множества оптимальных стратегий игроков в виде произвольных выпуклых комбинаций всех точек из множеств .

Вычислительное замечание. Проверять выполнение неравенств в пункте 11 нужно только для индексов , т.к. для индексов 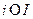и указанные неравенства в силу пунктов 6 и 7 алгоритма заведомо выполняются как равенства.

Приведем пример на использование описанного алгоритма.

Пример 5.1. Требуется найти общее решение (все решения) игры, заданной матрицей

.

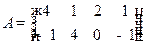Решение.

1. Матрица имеет седловую точку (1,4). Значит, цена , а крайние точки множеств запишутся, соответственно, в виде

. (5,21)

2. Убеждаемся, что третий столбец строго мажорирует четвертый. Полагаем и третий столбец в дальнейших вычислениях не используется, т.е. подматрицы, содержащие третий столбец, не рассматриваются (обратим внимание, что первый и второй столбцы матрицы тоже мажорируют четвертый столбец, но они мажорируют его не строго, при их вычеркивании можно потерять решения, тогда как задача состоит в отыскании всех решений).

3. Выбираем подматрицу . Находим ее определитель , обратную матрицу , сумму всех элементов обратной матрицы. Тогда . Это число не совпадает с уже известной ценой . Поэтому матрица отбраковывается.

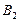4. Для подматрицы находим , , и подматрица отбраковывается.

5. Выбираем . Тогда , 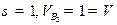. Поэтому из равенств (5.18) находим

, .

Так как при построении подматрицы не использовались первый и третий столбцы матрицы , то расширениями векторов до двух и четырехмерных векторов будут, соответственно,

. (5.22)

Проверяются условия следствия теоремы 2.2.1 оптимальности. Неравенства при и при заведомо выполняются как равенства. Убедимся, что и при первое из этих неравенств выполняется. Действительно, и . Значит, смешанные стратегии (5.22) являются оптимальными. Таким образом, общее решение записывается в виде выпуклой комбинации решений (5.21) и (5.22), т.е. в виде

, ,

где принимает любое значение из отрезка 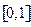. Задача решена.

Упражнение 1. Показать, что в игре с матрицей

множество 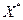состоит из единственной точки , а крайними точками множества оптимальных стратегий являются и .

Упражнение 2. При каких значениях в игре с матрицей

решение единственно, и при каких – имеются различные крайние точки множеств ? Найти указанные решения.

Следующий материал не является обязательным для чтения, но в нем приводится лемма, которая может существенно сократить перебор подматриц матрицы в случае, когда матрица имеет седловую точку.

Единичный вектор с единицей на 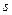-ом месте будем обозначать через .

Лемма 5.7. Если игра с 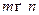- матрицей кроме седловой точки имеет оптимальные смешанные стратегии , то

, (5.23)

. (5.24)

Доказательство. Так как – седловая точка, то в силу леммы 5.6 векторы являются оптимальными смешанными стратегиями, а число – ценой игры.

Согласно теореме 2.2.1 оптимальности для оптимальных стратегий 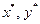и цены выполняются неравенства

. (5.25)

Кроме того, по определению седловой точки матрицы выполняются неравенства

, (5.26)

Если допустить, что условие (5.23) не выполняется, т.е. что в (5.26) выполняется строгое неравенство хотя бы для одного индекса 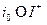, то получим

,

но это противоречит второму из неравенств (5.25) при . Таким образом, условие (5.23) доказано. Аналогично доказывается и (5.24). Лемма доказана.

Пример 5.2. Пусть игра определена матрицей

.

Определить все крайние точки множеств оптимальных стратегий.

Второй столбец матрицы мажорирует третий, но не строго. Поскольку требуется найти все решения, то второй столбец вычеркивать нельзя, т.к. можно потерять одно из решений.

Игра имеет седловую точку (1,3). Следовательно, цена и – крайние точки множеств оптимальных стратегий. Ни одну из подматриц , образованных из элементов первых двух столбцов матрицы можно не исследовать. Действительно, в соответствии с п.8 алгоритма требуется найти решение уравнения . Но ни одна из координат вектора не может быть отличной от нуля, т.к. тогда в силу леммы 5.2, по крайней мере, один из элементов должен равняться трем. Нетрудно понять, что и при выборе других подматриц не может получиться решений, отличных от уже найденного.

Л и т е р а т у р а

1. Н.Н.Воробьев. Теория игр (для экономистов-кибернетиков). М.,«Наука», 1985.

2. Э.Г.Давыдов. Исследование операций. Учебное пособие М., 1990.

3. Л.А.Петросян, Н.А.Зенкевич, Р.А.Семина. Теория игр. Учебное пособие, М., «Высшая школа», 1998.

4. Я.И.Заботин. Теория игр (Теоретические основы и игры с седловой точкой). Набережные Челны: филиал Казанского государственного университета, 2003.

5. Я.И.Заботин. Теория игр, Ч.2. (Решения матричных игр в смешанных стратегиях). Набережные Челны: филиал Казанского государственного университета, 2004.

Дополнительная литература

6. Э.Г.Давыдов. Методы и модели теории антагонистических игр. М.,Изд-во МГУ, 1978.

7. Г.Н. Дюбин, В.Г.Суздаль. Введение в прикладную теорию игр. М., «Наука», 1981.

8. Мак-Кинси Дж. Введение в теорию игр. М. «Физматгиз», 1960.

9. Г.Оуэн. Теория игр. М., «Мир», 1971.

С о д е р ж а н и е

В в е д е н и е ……………………………………………………………...…..3

§1. Мажорирующие и минорирующие стратегии.

Понижение порядка матрицы в матричной игре ………………………...….4

§2. Графо-аналитический метод решения игр с двустрочными и

двустолбцовыми матрицами…………………………………………………..8