П.3. Крайние точки множеств оптимальных стратегий

Лемма 5.4 (О крайних точках). Пусть в игре, определенной - матрицей

1) , где , – крайние точки множеств оптимальных стратегий , соответственно,

2) цена ,

3) ,

4) 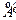– подматрица матрицы , стоящая на пересечении первых строк и первых столбцов.

Тогда первые 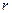строк и 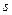столбцов в матрице 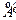линейно независимы.

Прежде, чем проводить доказательство, выпишем для наглядности матрицу , учитывая данные леммы (матрица выписана на следующей странице). В силу условий 1) леммы и теоремы о дополняющей нежесткости

(5.6)

Таким образом, . В соответствии с этим в матрице выделим подматрицы .

Для наглядности над матрицей выпишем стратегию , а справа от нее – стратегию .

Требуется доказать, что в матрице

первые 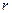строк и 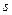линейно независимы.

Доказательство проведем способом от противного. Предположим, что в матрице 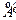первые 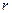строк линейно зависимы. Тогда найдутся такие числа , не все равные нулю, что

. (5.7)

Умножим каждое из этих равенств на , просуммируем их по и поменяем порядок суммирования. Так как при 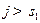, то суммирование по индексу 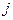можно распространить на все индексы от 1 до .

.

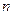Таким образом, получим равенство

. (5.8)

В силу третьего из условий леммы и равенства (5.8) выполняется равенство . А т.к. по условиям леммы , то

. (5.9)

Положим , , т.е.

,

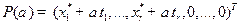где – числовой параметр. Убедимся, что для достаточно малых по абсолютной величине значений будет оптимальной смешанной стратегией первого игрока.

Поскольку при , то найдется такое , что для всех и . Кроме того, в силу (5.9)

.

Таким образом, является смешанной стратегией первого игрока при любых . Отметим, что

. (5.10) Если , то, учитывая (5.7) и (5.8), из (5.10) получим

. (5.11)

Если же 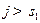, то в силу (5.6) и теоремы 2.2.1 оптимальности. Числа могут быть в данном случае ненулевыми, иметь разные знаки. Но их число конечно. Значит, найдется такое число , для которого правая часть неравенства (5.10) при любых останется не меньше, чем 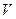, т.е. будут выполнены неравенства

для всех 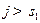. (5.12)

Таким образом, из (5.11) и (5.12) следует, что

для всех .

Отсюда и из теоремы 2.2.1 оптимальности векторы при являются смешанными оптимальными стратегиями. Следовательно, являются оптимальными смешанные стратегии и . Но , что невозможно, т.к. крайняя точка множества 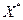по определению не может быть выпуклой комбинацией двух других отличных друг от друга точек множества 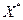. Полученное противоречие говорит о том, что предположение о линейной зависимости первых 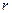строк матрицы 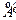не справедливо, т.е. они линейно независимы. Так как о линейной независимости первых 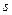столбцов матрицы доказывается аналогично, то можно считать доказательство леммы завершенным.

Теорема 5.1. Пусть игра, определенная матрицей , имеет цену и оптимальные смешанные стратегии 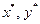. Для того чтобы 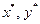были крайними точками множеств , соответственно, необходимо и достаточно, чтобы матрица содержала такую невырожденную подматрицу , что 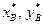были бы простыми оптимальными стратегиями в игре с матрицей и той же ценой .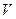

Доказательство. Необходимость. Дано, что 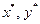являются крайними точками множеств , соответственно, Согласно теореме 3.1 перестановка строк в матрице приводит к перестановке координат в векторе с номерами, совпадающими с номерами переставленных строк, не изменяя цены игры. Аналогичное утверждение справедливо и для столбцов. Поэтому без ограничения общности рассуждений можно считать, что

.

Тогда справедливы равенства (5.6) в силу теоремы о дополняющей нежесткости. А поскольку такие равенства могут быть выполнены и для каких либо других индексов, то считаем, что выполнены условия 3) леммы 5.4. Таким образом, выполнены все условия леммы 5.4. Поэтому можно считать, что матрица разделена на подматрицы так же, как это сделано в этой лемме. Тогда согласно лемме 5.4 в матрице 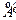первые 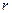строк и первые 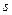столбцов линейно независимы. Но тогда в силу алгебраической леммы 5.1 существует такая квадратная невырожденная подматрица матрицы 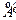ранга 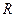, равного рангу матрицы 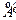, что . Из векторов 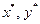построим векторы 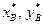. Заметим, что векторы 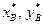получаются путем вычеркивания из векторов 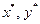нулевых координат. Значит, сумма координат в векторах 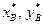остается равной единице. Следовательно, в игре с матрицей векторы 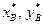являются смешанными стратегиями. Кроме того, для всех . А так как , то тем более эти равенства выполняются для всех . Аналогично, для всех и тем более для всех . Так как последние два равенства выполняются для одного и того же числа 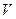, то в силу следствия теоремы 2.2.1 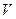является ценой, а 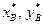– простыми оптимальными стратегиями в игре с матрицей . Необходимость доказана.

Достаточность. Отметим, что сейчас для доказательства имеются следующие данные:

1) – оптимальные смешанные стратегии в игре с матрицей и ценой ;

2) – такая квадратная невырожденная подматрица матрицы , что 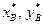являются простыми оптимальными смешанными стратегиями в игре с матрицей и ценой .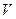

Докажем только, что – крайняя точка множества 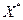, т.к. доказательство для точки 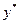проводится аналогично. Пусть элементы матрицы стоят на пересечении строк и столбцов с номерами из множеств , соответственно. Доказывая теорему от противного, предположим, что не является крайней точкой множества 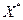. Тогда найдутся такие две точки

(5.13)

и число , что

, (5.14)

в частности

. (5.15)

Так как по условиям , – смешанные стратегии, то точка получена из вектора вычеркиванием нулевых координат. Заметим, что если , то из (5.14) следует . Таким образом, векторы получены из смешанных стратегий тоже путем вычеркивания нулевых координат. Значит, сумма координат у векторов осталась равной единице и, следовательно, – смешанные стратегии в игре с матрицей . Из (5.15) следует

. (5.16)

По условию 2)

, (5.17)

где – 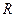-мерный вектор. Так как , то и для всех . Отсюда, , 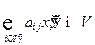для всех , или иначе

, . (5.18)

Учитывая (5.18), ни одна из координат векторов , не может быть меньше 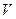. С другой стороны, в силу равенств (5.16) и (5.17) ни одна из координат этих векторов не может быть и больше 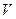. Следовательно, условия (5.18) выполняются как равенства , , т.е. стратегии являются решениями системы

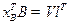(5.19)

линейных алгебраических уравнений. А так как матрицы является не вырожденной, то эта система имеет единственное решение. Значит , а т.к. при , то и , тогда как по условию (5.13) . Полученное противоречие завершает доказательство теоремы.

На основании теоремы 5.1 можно сформулировать алгоритм нахождения всех крайних точек многогранников , а следовательно, и общего решения игры. Отыскание крайних точек многогранников основано на следующем принципе. Выбирается квадратная невырожденная подматрица матрицы . Пусть подматрица находится на пересечении строк и столбцов с номерами , соответственно. Если игра с матрицей допускает простые смешанные стратегии 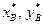, соответствующие числу , найденному согласно теореме 4.1, а расширения этих стратегий на местах вместе с числом удовлетворяют следствию теоремы 2.2.1, то – крайние точки многогранников а – цена игры. Если в процессе вычислений обнаружится, что нарушено одно из перечисленных требований, то подматрица не пригодна для построения крайних точек. Чтобы найти все крайние точки, требуется указанным приемом исследовать на пригодность все подматрицы матрицы .