 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
П.2. Структура множеств оптимальных смешанных стратегий
|
|
Лемма 5.2. Множества оптимальных смешанных стратегий игроков являются выпуклыми замкнутыми ограниченными многогранниками.
Согласно теореме 2.2.1 оптимальные стратегии  второго игрока удовлетворяют неравенствам
второго игрока удовлетворяют неравенствам
 ,
,  , (5.1)
, (5.1)
а т.к. эти стратегии смешанные, то они должны удовлетворять и условиям
 ,
,  . (5.2)
. (5.2)
Множество точек  , удовлетворяющих системе (5.1), (5.2) линейных неравенств и равенству, является многогранным по определению. Так как во всех условиях (5.1), (5.2) присутствует знак равенства, то легко доказывается замкнутость множеств точек, им удовлетворяющих. В силу (5.2) оно является ограниченным. Убедимся, что множество точек, удовлетворяющих (5.1) является выпуклым. Пусть
, удовлетворяющих системе (5.1), (5.2) линейных неравенств и равенству, является многогранным по определению. Так как во всех условиях (5.1), (5.2) присутствует знак равенства, то легко доказывается замкнутость множеств точек, им удовлетворяющих. В силу (5.2) оно является ограниченным. Убедимся, что множество точек, удовлетворяющих (5.1) является выпуклым. Пусть  – два произвольных решения системы (5.1). Тогда
– два произвольных решения системы (5.1). Тогда
 , (5.3)
, (5.3)
и для любого числа  в силу (5.3) выполняются условия
в силу (5.3) выполняются условия
 ,
,
откуда и следует выпуклость множества решений системы (5.1). Аналогично доказывается и выпуклость множеств точек, удовлетворяющих каждому из условий (5.2). Таким образом, множество оптимальных стратегий является пересечением выпуклых множеств, и следовательно, множеством выпуклым.
Аналогично доказывается выпуклость множества оптимальных стратегий первого игрока. Лемма доказана.
Определение 5.2. Пусть зафиксированы  точек
точек  пространства
пространства  . Множество точек
. Множество точек  , представимых в виде
, представимых в виде
 , (5.4)
, (5.4)
т.е. являющихся выпуклыми комбинациями этих точек, называется их выпуклой оболочкой.
Лемма 5.3. Всякий выпуклый замкнутый ограниченный многогранник является выпуклой оболочкой своих вершин.
Доказательство проведем индукцией по числу вершин. Для двух вершин
лемма очевидна. Допустим, что она доказана для многогранников с числом вершин не более  . Пусть теперь многогранник
. Пусть теперь многогранник  имеет
имеет  +1 вершину, и
+1 вершину, и  . Если точка
. Если точка  лежит на грани многогранника
лежит на грани многогранника  , то поскольку грань имеет вершин меньше, чем
, то поскольку грань имеет вершин меньше, чем  +1, то
+1, то  представляется в виде(5.4) в силу индукционного предположения.Пусть точка
представляется в виде(5.4) в силу индукционного предположения.Пусть точка  не лежит на грани многогранника
не лежит на грани многогранника  . Выберем какую-нибудь вершину многогранника
. Выберем какую-нибудь вершину многогранника  и обозначим ее
и обозначим ее  , проведем луч из точки
, проведем луч из точки  через
через  . Так как многогранник
. Так как многогранник  является ограниченным и замкнутым, луч пересечет границу в некоторой точке
является ограниченным и замкнутым, луч пересечет границу в некоторой точке  . Тогда найдется такое число
. Тогда найдется такое число  , что будет выполнено равенство
, что будет выполнено равенство
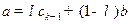 . (5.5)
. (5.5)
Так как точка  лежит на грани, а грань имеет число вершин меньшее, чем
лежит на грани, а грань имеет число вершин меньшее, чем  +1, то
+1, то  по индукционному предположению можно представить в виде выпуклой комбинации вершин грани, что можно записать в форме
по индукционному предположению можно представить в виде выпуклой комбинации вершин грани, что можно записать в форме
 .
.
Подставляя  в (5.5), Получим
в (5.5), Получим  в виде линейной комбинации точек
в виде линейной комбинации точек  , коэффициенты которой неотрицательны, при этом их сумма равна
, коэффициенты которой неотрицательны, при этом их сумма равна
 . Что и требовалось доказать.
. Что и требовалось доказать.
Таким образом, чтобы найти все оптимальные стратегии первого (второго) игрока, нужно найти все крайние точки, т.е. вершины множества
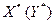 . Общее решение игровой задачи запишется после этого в виде выпуклой комбинации вершин множества
. Общее решение игровой задачи запишется после этого в виде выпуклой комбинации вершин множества 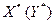 .
.
Дата публикования: 2014-10-20; Прочитано: 431 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
