 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Системы дифференциальных уравнений
|
|
Пример 34. Найти общее решение системы  (см. М-1540, стр. 40–41).
(см. М-1540, стр. 40–41).
Решение. Пусть  ,
, 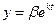 , подставим эти значения в систему:
, подставим эти значения в систему:
 .
.
Получим систему линейных уравнений относительно  . Чтобы эта система имела ненулевые (нетривиальные) решения, ее определитель должен быть равен нулю:
. Чтобы эта система имела ненулевые (нетривиальные) решения, ее определитель должен быть равен нулю:
 .
.
Это уравнение называется характеристическим и имеет два корня  . Возьмем сначала
. Возьмем сначала  и подставим в последнюю систему:
и подставим в последнюю систему:
 .
.
Полагая  , найдем
, найдем  и тогда
и тогда  ,
,  . Пусть теперь
. Пусть теперь  и тогда
и тогда
 .
.
Выбирая  , найдем
, найдем  и тогда
и тогда  ,
,  . Можно показать, что общим решением системы будет пара функций
. Можно показать, что общим решением системы будет пара функций 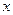 и
и 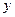 :
:
 ,
,  , где
, где  и
и  – произвольные постоянные.
– произвольные постоянные.
Дата публикования: 2014-10-20; Прочитано: 509 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
