 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Порядок числа. Первісні корені
|
|
Порядком числа 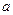 за модулем
за модулем  , при
, при  , називається найменше натуральне число
, називається найменше натуральне число  , яке задовільняє конгруентність
, яке задовільняє конгруентність 
Мають місце наступні властивості:
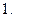 Якщо
Якщо  то
то 
 Числа
Числа  попарно непорівняльні за модулем
попарно непорівняльні за модулем  .
.
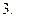 Якщо
Якщо 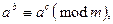 то
то 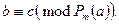

Число 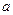 називається первісним коренем за модулем
називається первісним коренем за модулем  , якщо
, якщо 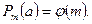
Кількість первісних коренів за простим модулем 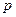 дорівнює
дорівнює 
Приклад. Знайти первісні корені за модулем 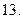
Так як  то первісних коренів
то первісних коренів 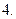 Порядки чисел за модулем
Порядки чисел за модулем 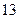 можуть бути лише дільниками числа
можуть бути лише дільниками числа 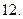 Число
Число  є первісним коренем, так як
є первісним коренем, так як  і тільки
і тільки 
Число 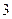 - не первісний корінь, так як уже
- не первісний корінь, так як уже 
Аналогічно перевіряють і наступні числа.
Відповідь: первісними коренями за модулем 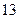 є числа
є числа 
Завдання. Знайти первісні корені за вказаним модулем.

Дата публикования: 2014-10-20; Прочитано: 2075 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
