З а д а ч а 12

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Пример 12. Решить систему уравнений методом Гаусса:

x + y - 3z = 2,

3x - 2y + z = - 1,

2x + y - 2z = 0.

Решение. Выпишем расширенную матрицу данной системы

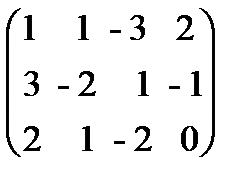
и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

~ ;

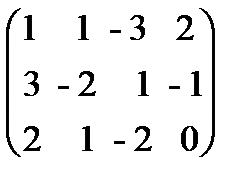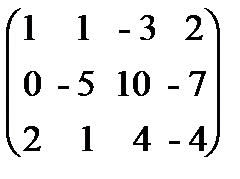б) третью строку умножим на (-5) и прибавим к ней вторую:

.

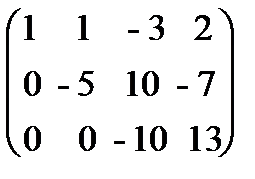В результате всех этих преобразований данная система приводится к треугольному виду:

x + y - 3z = 2,

-5y + 10z = -7,

- 10z = 13.

Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим
x = - 0,7.

Список литературы

1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии.- М.: Наука, 1982.

2. Клетеник Д.В. Сборник задач по аналитической геометрии. - СПб.: Профессия, 2002.

3. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры.- М.: ФИЗМАТЛИТ, 2005.

4. Проскуряков И. В. Сборник задач по линейной алгебре.- М; СПб.: ФИЗМАТЛИТ, 2001.

5. Фаддеев Д. К. Сборник задач по высшей алгебре. - СПб.: Лань, 1998.

6. Данко П. Е. Высшая математика в упражнениях и задачах. Ч 1.- М.: Высшая школа, 1999.

Содержание

Правила выполнения и оформления контрольной работы 3

Задания для контрольных работ 4

Пример выполнения контрольной работы 21

Список литературы 36

Учебное издание