 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Функция распределения
|
|
Функцией распределения F(x) называется вероятность того, что случайная величина x примет значение меньше x, где x– любое действительное число,
F(x) = р (x < х), где - ¥ < х < ¥
Свойства функции распределения:
1. 0 £ F(x) £ 1
2. При х  - ¥ F(x)
- ¥ F(x)  0
0
3. При х  + ¥ F(x)
+ ¥ F(x)  1
1
4. Вероятность попадания случайной величины в произвольный интервал действительной оси [x 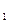 ,x
,x 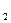 ] определяется формулой
] определяется формулой
 р(х1 £ x < х2) = F (х2) – F (х1)
р(х1 £ x < х2) = F (х2) – F (х1)
Докажем это свойство. Для этого рассмотрим событие (x < х2). Очевидно, что это событие можно записать в виде суммы:
(x < х2) = (х1 £ x < х2) + (x < х1), используя формулу сложения для несовместных событий, получим
р(x < х2) = р(х1 £ x < х2) + р(x < х1), откуда следует
F (х2) = р(х1 £ x < х2) + F (х1) или р(х1 £ x < х2) = F (х2)- F (х1).
5. Функция распределения F (х) – неубывающая функция на всей оси Ох, т.е.
если х2 > х1, то F (х2) ³ F (х1).
Действительно, пусть х2 > х1 , в пункте 5 показано, что для F (х2) справедливо равенство
F (х2) = р(х1 £ x < х2) + F (х1), а так как р(х1 £ x < х2) 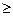 0, то отсюда следует,
0, то отсюда следует,
что F (х2) ³ F (х1).
6. Функция распределения непрерывна слева  , т.е.
, т.е.
 .
.
Зная закон распределения дискретной случайной величины, можно вычислить функцию распределения по формуле
F (x) =  ,
,
где суммирование распространяется на все те значения индекса i, для которых
 .
.
Пример 12. Построить функцию распределения для случайной величины, рассмотренной в Примере 11. Поскольку функция F(x) определена для всей действительных значений x, то рассмотрим последовательно интервалы:
1. х Î (- ∞; 0], F (x) = р(x < x) = 0, так как событие (x < x) на данном интервале является невозможным событием.
2. х Î (0; 1], F (x) = р(x = 0) = 1/4, здесь неравенству x < x удовлетворяет одно значение x = 0.
3. х Î (1; 2], F (x) = р(x = 0) + P (x = 1) = 1/4 + 1/2 = 3/4,здесь неравенству x < x удовлетворяют два значения x = 0 и x = 1.
4. х Î (2; ∞) F (x) = P (x = 0) + P (x = 1) + P (x = 2) = 1/4 + 1/2 + 1/4 = 1, на
этом интервале неравенству x < x удовлетворяют все значения случайной величины. Таким образом,
F(x) = 
График вычисленной функции приведен на Рис.7.

Рис. 7.
Квантилью порядка р распределения случайной величины x непрерывного типа называется действительное число x 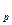 , удовлетворяющее уравнению р
, удовлетворяющее уравнению р  = р
= р
Дата публикования: 2014-10-19; Прочитано: 514 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
