 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лекция 6. Наивероятнейшее число появлений события
|
|
Наивероятнейшим числом появления события А в n независимых испытаниях называется такое число m 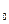 , для которого вероятность, соответствующая этому числу, не меньше вероятности каждого из остальных возможных чисел появления события А. Обозначим вероятность, соответствующую числу m
, для которого вероятность, соответствующая этому числу, не меньше вероятности каждого из остальных возможных чисел появления события А. Обозначим вероятность, соответствующую числу m 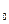 , через Р(n, m
, через Р(n, m 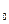 ), тогда согласно определению
), тогда согласно определению
Р(n, m 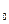 )
) 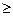 Р(n, m).
Р(n, m).
Для нахождения m 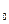 рассмотрим два неравенства
рассмотрим два неравенства

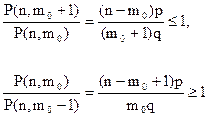
Решая совместно эти неравенства относительно m 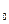 , получим, что m
, получим, что m 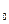 лежит винтервале единичной длины
лежит винтервале единичной длины
np – q 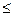 m
m 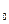
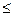 np + p.
np + p.
Пример 10. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,4 независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок.
В данной задаче n = 10, p = 0,4, q = 1-p = 1 – 0,4 = 0,6. Подставим эти данные
в приведенное выше неравенство
10 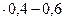
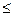 m
m 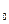
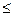 10
10  ,
,
3,4 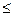 m
m 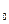
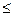 4,4,
4,4,
и окончательно, m 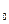 = 4. Наивероятнейшее число заявок равно 4.
= 4. Наивероятнейшее число заявок равно 4.
Найдем теперь вероятность получения четырех заявок по формуле Бернулли
Р(10,4) =  = 0,25.
= 0,25.
Статистическая оценка вероятности.
Длительные наблюдения над появлением или не появлением события А при большом числе независимых испытаний в ряде случаев показывают, что число
появлений события А подчиняется устойчивым закономерностям. Обозначим
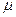 - число появлений события А,
- число появлений события А,
n - число испытаний,
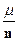 - частота появления события А при достаточно большом n сохраняет постоянную величину. Таким образом, под статистической вероятностью понимается относительная частота появления события А в n произведенных опытах.
- частота появления события А при достаточно большом n сохраняет постоянную величину. Таким образом, под статистической вероятностью понимается относительная частота появления события А в n произведенных опытах.
Статистическая вероятность обладает теми же свойствами, что и классическая вероятность, но при этом не требуется равновозможности исходов.
Наиболее общим является аксиоматическое определение вероятности, которое
сформулировал советский математик Колмогоров А.Н. в 1933 г..Однако это рассмотрение этого определения выходит за рамки данного курса лекций.
Дата публикования: 2014-10-19; Прочитано: 6496 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
