Комплексные числа

Комплексным числом называется выражение вида:

,

(алгебраическая форма числа z), где x и y – вещественные числа, i – мнимая единица, определяемая условием . 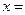Re – называется вещественной частью числа z, Im - мнимой частью z.

Число 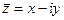называется сопряженным к z.

Если , ,

то

_.

_.

При делении двух комплексных чисел следует числитель и знаменатель умножить на – число, сопряженное к знаменателю.

Число r (рис. 16) называется модулем комплексного числа z и обозначается :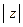

.

Угол называется аргументом комплексного числа z и обозначается Аrg , при этом .

Рис. 16.

Аргумент определяется неоднозначно, с точностью до слагаемого, кратного 2p: , где 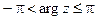– главное значение аргумента. поэтому необходимо учитывать следующие соотношения:

при x > 0;

при x < 0, y ³ 0;

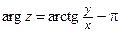при x < 0, y < 0.

Так как , то комплексное число z можно представить в виде:

.

Такая запись называется тригонометрической формой комплексного числа z.

Если заданы два комплексных числа в тригонометрической форме и , то

,

,

Корнем n-ой степени из комплексного числа z называется такое комплексное число , что

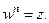
Обозначение для корня: . Корень n -ой степени из числа имеет n различных значений, определяемых по формуле:

,

.

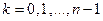Геометрически числа располагаются в вершинах правильного n -угольника, вписанного в круг радиуса с центром в начале координат.

Пример 1.10. Дано комплексное число

1) Записать число z в алгебраической и тригонометрической формах.

2) Найти .

Решение.

1)

- алгебраическая форма.

Так как число z находится в 4-й четверти, то

Таким образом, тригонометрическая форма числа z:

2)

где k принимает значения 0, 1, 2.

При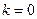

.

При

.

При

.