Линейная алгебра

1.1.1. Определители

Определителем 2-го порядка с элементами a ₁₁, a ₁₂, a ₂₁, a ₂₂ называется число, которое обозначается и вычисляется следующим образом:

Определителем 3-го порядка с элементами называется число, которое обозначается и вычисляется следующим образом:

Определителем порядка n с элементами

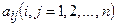
называется число D, которое обозначается следующим образом:

и вычисляется разложением по какой-нибудь строке или какому-нибудь столбцу. При этом при разложении по строке с номером i используется формула

где A_ij – алгебраическое дополнение элемента a_ij, то есть определитель порядка , получаемый из определителя D вычеркиванием i -й строки и j -го столбца, взятый со знаком

Аналогично записывается формула для разложения по столбцу с номером j:

Эти рекуррентные формулы позволяют последовательно понижать порядок вычисляемых определителей, сводя все к простым случаям определителей 2-го или 3-го порядков.

Пример 1.1. Вычислить определитель

.

Решение. Раскладывая по элементам второго столбца, имеем

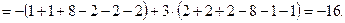
1.1.2. Матрицы

Матрицей A размера () называется прямоугольная таблица чисел вида

,

содержащая m строк и n столбцов. Числа a_ij называются элементами матрицы.

При матрица называется квадратной порядка n.

Для квадратной матрицы A можно рассматривать ее определитель, который обозначается или .

Если определитель матрицы A отличен от нуля , то матрица A называется невырожденной или неособой.

Матрица называется транспонированной к матрице A, если столбцы матрицы A заменить ее строками (или строки – столбцами).

Пример 1.2. Найти транспонированные матрицы к матрицам А и В.

.

Решение. .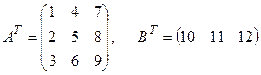

Если A и B – матрицы одинакового размера, то их суммой называется матрица того же размера, элементы которой равны сумме соответствующих элементов матриц A и B.

Для произвольного числа матрицей называется матрица, размер которой совпадает с размером матрицы A и элементы которой получаются из соответствующих элементов матрицы A умножением на .

Если даны матрица A размера и матрица B размера то есть число столбцов матрицы A равно числу строк матрицы В, то произведением матриц A и В называется матрица размера элементы с_ij которой вычисляются по формуле

то есть для вычисления элемента с_ij матрицы C, стоящего на пересечении i -ой строки и j -го столбца, следует умножить элементы i -ой строки матрицы A на соответствующие элементы j -го столбца матрицы B и сложить все полученные результаты.

Пример 1.3. Найти произведение матриц . Можно ли умножить матрицу на матрицу ?

, .

Решение. Количество столбцов матрицы А равно количеству строк матрицы В, поэтому

.

Количество столбцов матрицы В не равно количеству строк матрицы А, поэтому произведение матриц не определено.

Пример 1.4. Найти произведения матриц и .

и .

Решение. .

.

Квадратная матрица порядка n вида

называется единичной матрицей порядка n.

Если A – квадратная матрица порядка n, то обратной матрицей называется такая квадратная матрица того же порядка, что

и

Для того, чтобы квадратная матрица A имела обратную матрицу , необходимо и достаточно, чтобы она была невырожденной, то есть

,

при этом вычисляется по формуле

.

Здесь – определитель матрицы A, 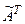– транспонированная матрица алгебраических дополнений.

Пример 1.5. Для матрицы найти обратную.

Решение. Вычислим определитель матрицы:

Найдем алгебраические дополнения:

поэтому матрица алгебраических дополнений имеет вид

и обратная матрица

.

Проверка:

.

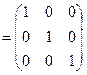Нетрудно убедиться, что и .