 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Прямая на плоскости
|
|
Общее уравнение прямой на плоскости:
 .
.
Если 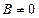 , обозначим
, обозначим  и получим уравнение прямой с угловым коэффициентом:
и получим уравнение прямой с угловым коэффициентом:
 .
.
Геометрический смысл параметров k и b:  , где
, где  – угол, образованный прямой с осью Ox,
– угол, образованный прямой с осью Ox,  – отрезок, отсекаемый прямой на оси Oy (рис. 6).
– отрезок, отсекаемый прямой на оси Oy (рис. 6).

Рис. 6.
Уравнение прямой с угловым коэффициентом k и проходящей через точку M 1(x 1; y 1):
 .
.
Уравнение прямой, проходящей через две точки M 1(x 1; y 1) и M 2(x 2; y 2):
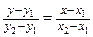 ;
;
угловой коэффициент этой прямой  .
.
Если в общем уравнении прямой 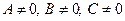 , то, полагая
, то, полагая  , получим уравнение прямой в отрезках:
, получим уравнение прямой в отрезках:
 ,
,
здесь а и b – отрезки, отсекаемые прямой на осях Ox и Oy соответственно (рис. 7).

Рис. 7.
Если даны две прямые  и
и  , то угол
, то угол  между ними (острый) определяется по формуле
между ними (острый) определяется по формуле
 .
.
Условие параллельности этих прямых:  .
.
Условие перпендикулярности прямых:  .
.
Расстояние  от точки M 0(x 0; y 0) до прямой
от точки M 0(x 0; y 0) до прямой

вычисляется по формуле

Пример 1.7. Даны вершины треугольника А (0;1), B (6;5) и С (12;–1). Составить уравнение высоты треугольника, проведенной из вершины С (рис. 8).

Рис. 8.
Решение. Составим уравнение прямой АВ:  или
или 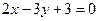 . Угловой коэффициент прямой АВ равен
. Угловой коэффициент прямой АВ равен  , следовательно, угловой коэффициент высоты
, следовательно, угловой коэффициент высоты  , проведенной из вершины С, равен
, проведенной из вершины С, равен  (так как прямые перпендикулярны). Уравнение высоты
(так как прямые перпендикулярны). Уравнение высоты  имеет вид:
имеет вид:
 или
или 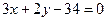 .
.
Дата публикования: 2014-10-19; Прочитано: 412 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
