Кривые второго порядка на плоскости

Общее уравнение кривой второго порядка на плоскости имеет вид:

.

Любая кривая второго порядка – это либо эллипс (частный случай – окружность), либо гипербола, либо парабола.

Если в уравнении , то оно преобразуется выделением полных квадратов:

и после введения соответствующих обозначений приводится к одному из следующих видов:

1. – уравнение эллипса с центром в точке 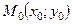и полуосями а и b (рис. 11).

Рис. 11.

Если , то получаем окружность радиуса R с центром в точке .

2. – уравнение определяет гиперболу с центром в точке М ₀ . Для знака плюс, например, точки , – вершины гиперболы (рис. 12).

Рис. 12.

Гипербола имеет две асимптоты: .

3. Если или , то получается уравнение параболы, например, для :

.

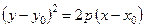Рис.13.

Точка 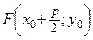называется фокусом параболы, а прямая называется директрисой параболы (рис. 13).

Кроме указанных, возможны некоторые вырожденные случаи (когда уравнение определяет пару пересекающихся, параллельных или совпадающих прямых) и мнимые случаи.

Пример 1.9. Составить уравнение и построить линию, расстояния каждой точки которой от точки A (0;–2) и от прямой относятся как 4:5.

Решение. Возьмем точку на искомой кривой. Тогда точка К, лежащая на прямой , имеет координаты (МК – расстояние от М до прямой).

Рис. 14.

Из условия задачи известно, что АМ: МК =4:5.

Используя формулу для вычисления расстояния между двумя точками, получим

.

Решим это уравнение:

, ,

,

,

, .

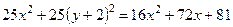Получили каноническое уpавнение эллипса с центром в точке . Полуоси эллипса: , (рис.15).

Рис. 15.