Теоретические сведения. Чтобы устранить двузначность корня k-й степени из числа а, вводится понятие арифметического корня

Чтобы устранить двузначность корня k- й степени из числа а, вводится понятие арифметического корня. Арифметическим кор­нем k-й степени из числа а (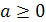) называется неотрица­тельное число b, k- я степень которого равна а, где 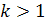- натуральное число.

Преобразования арифметических корней

1. Корень k- й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где 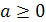, 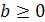(правило извлечения корня из произведения).

2. Если 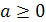, , 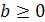то (правило извлечения корня из дроби).

3. Если 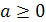, , 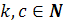, 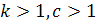то (правило извлечения корня из корня).

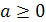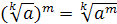4. Если , то (правило возведения корня в степень).

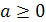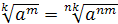5. Если , то , где 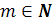, , 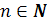т.е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.

6. Если 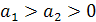, то 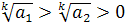, т. е. большему положи­тельному подкоренному выражению соответствует и большее зна­чение корня.

Все указанные выше формулы часто применяются в обрат­ном порядке (т. е. справа налево).

7. Правило вынесения множителя из-под знака корня. При , .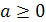

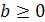
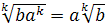8. Применение тождеств сокращенного умножения к действи­ям с арифметическими корнями:

1) ;

2) ;

3) .

Множитель, стоящий перед корнем, называется его коэф­фициентом.

Корни (радикалы) называются подобными, если они имеют одинаковые показатели корней и одинаковые подкоренные выра­жения, а отличаются только коэффициентом. Чтобы судить о том, подобны данные корни (радикалы) или нет, нужно привести их к простейшей форме.

Пример 1. Найти значение выражения: .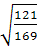

Решение. По правилу извлечения корня из дроби имеем:

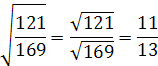
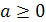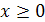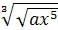Пример 2. Упростить при , 1) ; 2) .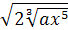

Решение. При извлечении корня из корня показатели корней перемножаются, а подкоренное выражение остается без изменения.

1) .

Если перед корнем, находящимся под корнем, имеется коэффициент, то прежде чем выполнить операцию извлечения корня, вводят этот коэффициент под знак радикала, перед которым он стоит.

2) .

Пример 3. Возвести в степень: 1) ; 2) .

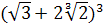Решение. При возведении корня в степень показатель корня остается без изменения, а показатели подкоренного выражения умножаются на показатель степени.

1) 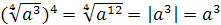(так как 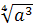определен, то );

2) Выражение в скобках, представляющее сумму двух различных радикалов, возведем в куб и упростим:

.

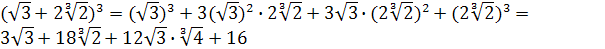Поскольку 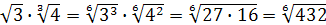, имеем:

.

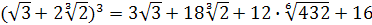Пример 4. Исключить иррациональность в знаменателе: 1) 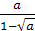; 2) .

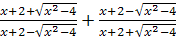Решение. Для исключения иррациональности в знаменателе дроби нужно подыскать простейшее из выражений, которое в произведении со знаменателем дает рациональное выражение, и умножить на подысканный множитель числитель и знаменатель данной дроби.

В более сложных случаях уничтожают иррациональность не сразу, а в несколько приемов.

1) В выражении 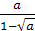должно быть 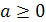и 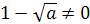. Умножая числитель и знаменатель дроби на 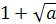, получим:

.

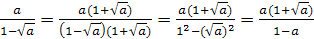2) Приведем дроби к общему знаменателю:

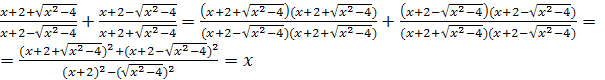. Решая данный пример, мы должны иметь в виду, что каждая дробь имеет смысл, т.е. знаменатель каждой дроби отличен от нуля. Кроме того, .