 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теоретические сведения. Иррациональным числом называют бесконечную десятичную непериодическую дробь, например, 0,131331333125
|
|
Иррациональным числом называют бесконечную десятичную непериодическую дробь, например, 0,131331333125.... Известные в математике число 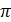 , число
, число 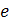 (основание натуральных логарифмов) также являются числами иррациональными.
(основание натуральных логарифмов) также являются числами иррациональными.
Другой пример, приводящий к понятию иррационального числа, дает следующая теорема: «Не существует рационального числа, квадрат которого равен двум». Иными словами, решение уравнения 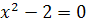 невозможно на множестве рациональных чисел. Корнями такого уравнения являются иррациональные числа
невозможно на множестве рациональных чисел. Корнями такого уравнения являются иррациональные числа  .
.
Любое рациональное число вида  , где
, где 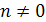 , может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
, может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
Корнем k -й степени, где  и
и 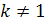 , из действительного числа а называется действительное число х, k -я степень которого равна а.
, из действительного числа а называется действительное число х, k -я степень которого равна а.
Корень k -й степени из числа а обозначается символом  . Согласно определению
. Согласно определению 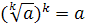 .
.
Нахождение корня k -й степени из числа а называется извлечением корня. Число k называют показателем корня, число а — подкоренным выражением.
Заметим, что 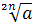 , где
, где 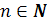 и
и 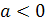 , не существует. Например, выражения
, не существует. Например, выражения 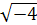 ,
, 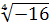 не имеют смысла. Корень нечетной степени извлекается и из отрицательного числа. Например
не имеют смысла. Корень нечетной степени извлекается и из отрицательного числа. Например 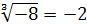 , так как
, так как 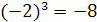 .
.
Рациональные и иррациональные числа образуют множество действительных чисел.
Действительным числом называется бесконечная десятичная дробь, т.е. дробь вида 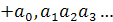 или
или 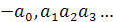 , где
, где 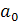 - целое неотрицательное число, а каждая из букв
- целое неотрицательное число, а каждая из букв  - это одна из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- это одна из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Модулем (абсолютной величиной) действительного числа а называется само это число, если 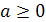 , и противоположное число -а, если
, и противоположное число -а, если 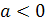 . Модуль а обозначается
. Модуль а обозначается 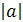 . Итак,
. Итак,
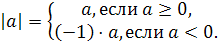
Геометрически 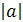 означает расстояние на координатной прямой от точки, изображающей число а, до начала отсчета.
означает расстояние на координатной прямой от точки, изображающей число а, до начала отсчета.
Модуль нуля равен нулю.
Если 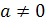 , то на координатной прямой существуют две точки а и - а, равноудаленные от нуля (рис. 1), модули которых равны.
, то на координатной прямой существуют две точки а и - а, равноудаленные от нуля (рис. 1), модули которых равны.

Рис. 1 Координатная прямая
Пример1. Записать выражение без знака модуля:
1) 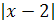 ; 2)
; 2) 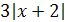 ; 3)
; 3) 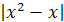 ; 4)
; 4) 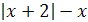 .
.
Решение. 1) Здесь под 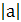 имеется в виду
имеется в виду 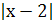 . По определению модуля имеем:
. По определению модуля имеем:
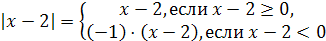
или 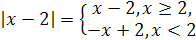 .
.
2) Здесь под 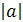 имеется в виду
имеется в виду 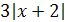 . По определению модуля имеем:
. По определению модуля имеем:
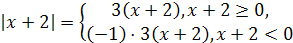
или 3 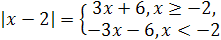 .
.
3) Здесь под 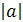 имеется в виду
имеется в виду 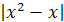 . По определению модуля имеем:
. По определению модуля имеем:
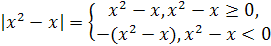 .
.
4) Здесь под 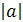 имеется в виду
имеется в виду 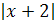 , выражение
, выражение 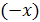 от модуля не зависит.
от модуля не зависит.
Используем определение для раскрытия модуля:
 ,
,
или 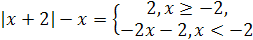 .
.
Пример 2. При каких значениях х данное выражение имеет смысл:
1) 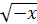 ; 2)
; 2) 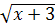 ; 3)
; 3) 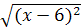 .
.
Решение. 1) Из определения арифметического квадратного корня следует, что 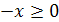 . Умножим обе части этого неравенства на -1 и получим
. Умножим обе части этого неравенства на -1 и получим 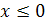 .
.
2) На основании определения арифметического квадратного корня имеем 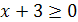 , или
, или 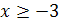 .
.
3)  для всех
для всех  , значит, выражение имеет смысл при любом значении х.
, значит, выражение имеет смысл при любом значении х.
Пример 3. При каких значениях х справедливо равенство 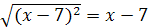 ?
?
Решение. Так как 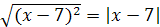 , то исходное равенство примет вид
, то исходное равенство примет вид 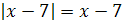 . А это равенство справедливо только при
. А это равенство справедливо только при 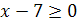 , т. е. при
, т. е. при  .
.
Пример 4. Упростить выражение:
1) 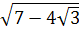 ; 2)
; 2) 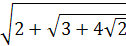 .
.
Решение. 1) Обратим внимание, что 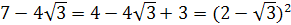 . Поэтому
. Поэтому 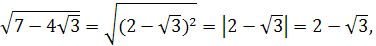 так как
так как 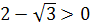 .
.
2) Выражение 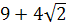 представим так:
представим так:  . Тогда
. Тогда 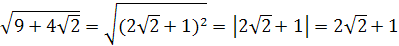 .
.
Теперь выражение 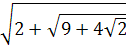 примет вид
примет вид 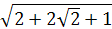 . Упростим его:
. Упростим его:
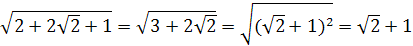 .
.
Дата публикования: 2014-11-18; Прочитано: 437 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
