Выбор порядка проведения операции контроля в условиях ограничений частичной упорядоченности

Особенно острый дефицит общего времени на контроль испытывается обычно на этапе предполетной подготовки при проведении тесто­вого контроля работоспособности бортового оборудования. По­этому минимизация общего времени контроля всех параметров объекта за счет расчленения процедур контроля на модули и оп­тимального их проведения представляет практическую ценность.

Модули Z_i включают в себя непосредственно длительность контрольных операций t_{i ,}а также интервалы t_ij, к примеру ожидания переходных процессов, или длительности настроек при переходе от операции z_i к z_j, а также времени для переключения соответствующих цепей коммутации. Минимизация общего времени контроля T_k заключается в оптимальном заполнении указанных времен ожидания контрольно-измерительными операциями других модулей. Однако при этом необходимо, в некоторых случаях, учитывать частичную априорную технологическую упорядоченность модулей в виде ограничений на отношение порядка U, которые задаются в виде графа G(Z,U)
, к примеру рис. 2.1, где вершина Z₀ (мажоранта), для которой t₀ и t _0i равны нулю, фиксирует начало процесса построения множества возможных вариантов (допустимых) решений W(S₀). Висячая вершина графа (в примере Z _v) фиксирует окончание процесса ветвление вариантов.

Путем в графе G(Z,U) является последовательность ориенти­рованных дуг U, которые выражают ограничения порядка между вершинами на этом пути. Длина пути от начала процесса (мажоранты) до некоторой вершины соответствует глубине распо­ложения проверяемого подмножества и равна числу дуг на нем. В дальнейшем, говоря о глубине расположения проверяемого под­множества, подразумевается нахождение соответствующей вершины на некотором k -м уровне графа G, что предполагает пре­образование его в дерево. Такое преобразование необходимо пото­му, что граф, построенный из непосредственного анализа объекта, обычно получается слишком сложным и нуждается в предваритель­ном упорядочении.

Поставленная задача примыкает по своей сущности к классу экстремальных комбинаторных задач. В принципе она может быть решена простым перебором вариантов, однако необходимый при этом объем вычислений не позволяет получить оптимального результата даже в простейшем случае.

Перспективным способом решения оптимизационных задач контроля является метод ветвей и границ.

Идея этого метода заключается в следующем. Множест­во W(S₀) всех допустимых вариантов решения разбивается на непересекающиеся подмножества W(S_k), которые, в свою очередь, разбиваются на подмножества меньшей мощности W(S_i) до полу­чения подмножества W(S_ν), состоящего из единственного вариан­та. Процесс разбиения множества допустимых вариантов W(S₀) на их непересекающиеся подмножества называется ветвлением вари­антов, а получаемое при этом дерево D (S,Г_D) - деревом реше­ний (ветвлений) (рис. 2.2). Здесь S={S_k} множество вершин этого дерева, а Г_D отношение порядка на этом множестве. Каждой вершине дерева решений соответствует некоторый модуль z_i Î Z графа G (Z,U), а любой путь по дереву определяет соответствующий граф очередности V[Y(S), Г_V]. Множество вершин Y(S) описывает определенный вариант процесса (незаконченный, если YÌZ и законченный, если Y=Z), а Г_V отношение порядка на множестве Y(S).

Пусть Y(S_k) —множество вершин в графе очередности V, соот­ветствующих пути от S₀ до S_k в дереве D. Из каждой вершины S_k выходит столько ветвей, сколько допустимых модулей (претенден­тов для упорядочения) имеется в подмножестве Z\Y(S_k). Множе­ство допустимых на каждом шаге процесса ветвления модулей об­разует фронт упорядочения. Наглядное представление об образо­вании фронта упорядочения дает преобразованный граф G. Очевидно, на первом шаге процесса построения дерева D фронт упорядочения образуют вершины, ко­торые соединены с мажорантой одной дугой, на втором шаге к ним добавляются все последователи включенной в D вершины, в кото­рую не входят дуги из других вершин, и т. д. Hа произвольное ша­ге фронт упорядочения образуют те модули, для которых Г_о ^-1z_i= .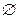

Метод ветвей и границ предполагает построение дерева ветвле­ния вариантов D и фактически представляет собой процедуру пос­ледовательного анализа вариантов, дополненную прогнозировани­ем такого направления поиска, в котором с наибольшей вероятно­стью находится оптимальное решение. Идея прогнозирования за­ключается в оценке нижних границ минимизируемой целевой функ­ции для разветвляемых подмножеств

W(S_k). На каждом шаге, ветвление продолжается из вершины, имеющей минимальную оцен­ку. Задача сводится к отысканию па дереве конечной вершины, со­ответствующей оптимальному допустимому решению со значением целевом функции, меньшим или равным оценкам висячих вершин дерева D.

Как показывает практика применение метода ветвей и границ, его эффективность значительно зависит от способа представления решения в виде дерева вариантов и метода оценки нижней границы целевой функции.

Для минимизации T_k этот метод может быть применен следующим образом.

На основе исходной информации, заданной графом G, строится 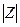-размерные квадратные матрицы || b_ij || и || d_ij || такие, что

(2.2)

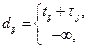
(2.3)

Вводится понятие T_н (z_k)- наиболее раннее время начала модуля z_k

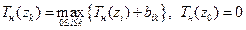. (2.4)

Обозначим H ={ L_ij }—множество всех независимых путей (путей, отличающихся друг от друга хотя бы одной дугой) на графе, ведущих от вершины z_i к z_j и 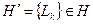— множество всех не­зависимых путей, ведущих от вершины z_k к миноранте (висячей вершине графа G).

Некоторый путь L_k по этому дереву представляет собой частичный подграф G (Z_k, U_k), при этом длина пути:

T (L_k) = 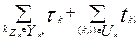(2.5)

Длина критического пути вычисляется из рекуррентного соотношения наиболее длинного пути из вершины z_k к миноранте графа G.

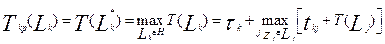. (2.6)

На основании приведенных выражений процесс преобразования графа G (Z,U) в граф очередности V =(Y,Г_D) может быть интерпретирован следующим образом. Находится для каждой вер­шины S_k 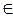S дерева ветвления вариантов D множество

	(2.7)

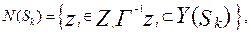
где 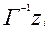- предшественники вершины z_i на множестве Y (S_k) графа V,

которое определяет фронт упорядочения. Согласно априорной час­тичной упорядоченности модулей, выражаемой отображением Г_k, очередной модуль при пошаговом построении графа D может быть выбран только из |N(S_k)|, выражающего мощность фронта упо­рядочения.

На основе (2.6) можно записать выражение для оценки нижних границ для произвольного подмножества вариантов W(S_k) в следующем виде:

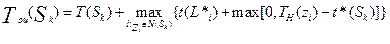. (2.8)

T_оц(S_k) = t^*(S_k) + max { t(L^*_i) +max[ 0,T_H(z_i)-t^*(S_k) ]},

i:z_iЄN(S_k)

где t^*(S_k)=Στ_i + Στ_kl.

i:z_i Є-Y(S_k) (k,l Є Г_D)

На каждом шаге для дальнейшего разветвления выбирается вершина S^*_k, для которой справедливо равенство

Т_оц (S_k)= min { Т_оц (S_k) } | S_k Є S^* }, S_k

где S^* Є S - подмножество вершин , из которых можно продолжать ветвление на данном этапе построения дерева очередности.

Выбранная вершина S_k Є S^* в итоге получает N (S_k) последователей, определяющих разбиение множества возможных вариантов W (S_k) на N (S_k) непересекающихся подмножеств.

При достижении в процессе ветвления W (S_ν), состоящего из единственного варианта V [ Y (S_ν), Г_ν) ], при этом Y (S_ν)= Z и последний вариант будет оптимальный, если

T_оц(S_ν) ≤ { Т_оц (S_k) } | S_k Є S^* }. (2.9)

Рассмотрим применение данного алгоритма на численном примере.

Допустим задан следующий граф G(Z,U) (рис. 2.1) и таблицы длительности операций (таблица 2.1), и времён переходов (таблица 2.2):

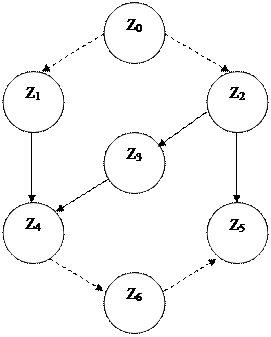Рис. 2.1 – Граф исходного множества модулей

Таблица 2.1 – Длительность операций

Вершины zi	Z1	Z2	Z3	Z4	Z5
Длительность τi

Таблица 2.2 – Минимальное время задержки между модулями

Дуги графа U	(0,1)	(0,2)	(1,4)	(2,3)	(2,5)	(3,4)	(4,6)	(5,6)
Длительность перехода tij

Требуется определить оптимальную последовательность проведения проверок с использованием метода ветвей и границ.

2.3.1. Составляется граф D (рис. 2.2), заключающий в себе все множество вариантов последовательностей проверок некоторого объекта контроля (рис. 2.1)

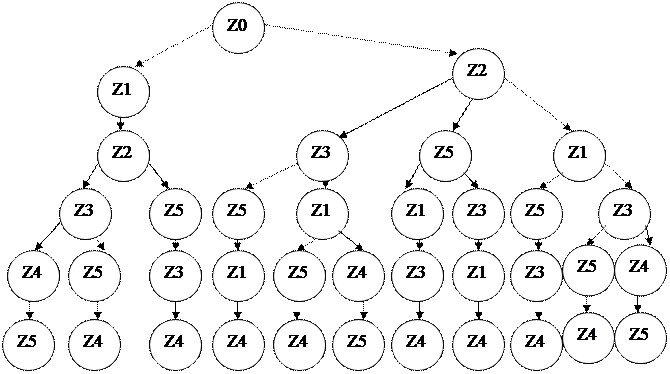
Рисунок 2.2 – Дерево ветвления вариантов.

2.3.2. На основе исходных данных стоится z -размерная квадратная матрица b_ij по формуле (2.2):

2.3.3. Определяется наиболее раннее время начала модуля z_k, используя формулы (2.3) и (2.4):

T_H(z₀) = 0;

T_H(z₁) = 0;

T_H(z₂) = 0;

T_H(z₃) = max {T_H(z₂) + b₂₃} = 0 + 16 = 16;

T_H(z₄) = max {T_H(z₁) + b₁₄ , T_H(z₃) + b₃₄} = max {0 + 18, 16 + 12} = 28;

T_H(z₅) = max {T_H(z₂) + b₂₅} = 0 + 8 = 8;

T_H(z₆) = max {T_H(z₄) + b₄₆ , T_H(z₅) + b₅₆} = max {28 + 3, 8 + 8} = 31;

2.3.4. Определяются длины критических путей юля каждой из вершин z_i, которые ведут от вершины z_i к миноранте по формулам (2.5) и (2.6):

T[L*(z₀)] = τ₀ +τ₂ +τ₃ +τ₄ +t₀₂ +t₂₃ +t₃₄ +t₄₆ = 31

T[L*(z₁)] = τ₁ +τ₄ +t₁₄ +t₄₆ = 21

T[L*(z₂)] = τ₂ +τ₃ +τ₄ +t₂₃ +t₃₄ +t₄₆ = 31

T[L*(z₃)] = τ₃ +τ₄ +t₃₄ +t₄₆ = 15

T[L*(z₄)] = τ₄ +t₄₆ = 3

T[L*(z₅)] = τ₅ +t₅₆ = 8

T[L*(z₀)] = τ₆ = 0

Полученные данные сводятся в таблицу (таблица 2.3)

Таблица 2.3

Zi	τi	TH(zi)	T[L*(zi)]	U	tij
z0				(0,1)
z1				(0,2)
z2				(1,4)
z3				(2,3)
z4				(2,5)
z5				(3,4)
z6				(4,6)
				(5,6)

2.3.5. Рассчитывается по шагам оценка нижних границ для подмножества вариантов W(S_k) c использованием формул (2.7), (2.8) и (2.9)

ШАГ 1

S₀, z₀;

N (S₁) = { z₁, z₂ };

Y (S₁) = { z₀ };

t*(S₀) = τ ₀ = 0;

T _оц(S₀) = t*(S₀) + max { t (L*₁) + max[0, T_H (z₁) – t* (S₀)], t (L*₂) + max[0, T_H (z₂) – t* (S₀)]} = 0 + max {21 + max[0,0];31 + max[0,0]} = 31.

ШАГ 2

S₁, z₁;

N (S₁) = { z₂ };

Y (S₁) = { z₀,z₁ };

t* (S₁) = τ₀ + t₀₁ + τ₁ = 2;

T_оц (S₁) = t* (S₁) + max { t (L*₂) + max[0, T_H (z₂) – t* (S₁)]} = 2 + max {31 + max[0,-2]} = 33.

ШАГ 3

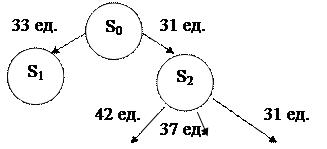
S₂, z₂;

N (S₂) = { z₃,z₅, z₁ };

Y (S₂) = { z₀, z₁ };

t* (S₂) = τ₀ + t₀₂ + τ₂ = 4;

T_оц (S₀) = t* (S₂) + max { t (L*₃) + max[0, T_H (z₃) – t* (S₂)], t (L*₅) + max[0, T_H (z₅) – t* (S₂)], t (L*₁) + max[0, T_H (z₁) – t* (S₂)]} = 4 + max {15 + max[0, 16-4],8 + max[0,8-4],21 + max[0,0-4]} = 4 + max{27, 12, 21} = 31.

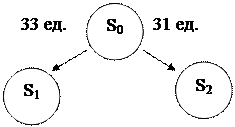Рис. 2.3 – Результат ветвления шагов 1 3

ШАГ 4

S₃, z₃;

N (S₃) = { z₁,z₅ };

Y (S₃) = { z₀, z₂, z₃ };

t* (S₃) = τ₀ + t₀₂ + τ₂ + t₂₃ + τ₃ = 21;

T_оц (S₃) = t* (S₃) + max { t (L*₁) + max[0, T_H (z₁) – t* (S₃)], t (L*₅) + max[0, T_H (z₅) – t* (S₃)]} = 21 + max {21 + max[0, 0-21],8 + max[0,8-21]} = 21 + max{21, 8} = 42.

ШАГ 5

S₄, z₅;

N (S₄) = { z₁,z₃ };

Y (S₄) = { z₀, z₂, z₅ };

t* (S₄) = τ₀ + t₀₁ + τ₂ + t₂₅ + τ₅ = 16;

T_оц (S₄) = t* (S₄) + max { t (L*₁) + max[0, T_H (z₁) – t* (S₄)], t (L*₃) + max[0, T_H (z₃) – t* (S₄)]} = 16 + max {21 + max[0, 0-16],15 + max[0,16-16]} = 16 + max{21, 15} = 37.

ШАГ 6

S₅, z₁;

N (S₅) = { z₅,z₃ };

Y (S₅) = { z₀, z₂, z₁ };

t* (S₅) = τ₀ + t₀₂ + τ₂ + t₂₁ + τ₁ = 6;

T_оц (S₅) = t* (S₅) + max { t (L*₅) + max[0, T_H (z₅) – t* (S₅)], t (L*₃) + max[0, T_H (z₃) – t* (S₅)]} = 6 + max {8 + max[0, 8-6],15 + max[0,16-6]} = 6 + max{10, 25} = 31.

42 eд.

31 eд.

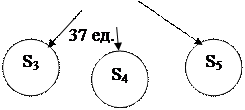Рис. 2.4 – Результат ветвления шагов 1 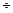6

ШАГ 7

S₆, z₅;

N (S₆) = { z₃ };

Y (S₆) = { z₀, z₂, z₁, z₅ };

t* (S₆) = τ₀ + t₀₂ + τ₂ + t₂₁ + τ₁ + t₁₅ + τ₅ = 16;

T_оц (S₆) = t* (S₆) + max { t (L*₃) + max[0, T_H (z₃) – t* (S₆)]} =16 + max {15 + max[0, 16-16]} = 31.

ШАГ 8

S₇, z₃;

N (S₇) = { z₅, z₄ };

Y (S₇) = { z₀, z₂, z₁, z₃ };

t* (S₇) = τ₀ + t₀₂ + τ₂ + t₂₁ + τ₁ + t₁₃ + τ₃ = 11;

T_оц (S₇) = t* (S₇) + max { t (L*₅) + max[0, T_H (z₅) – t* (S₇)], t (L*₄) + max[0, T_H (z₄) – t* (S₇)]} = 11 + max {8 + max[0, 8-11],3 + max[0,28-11]} = 11 + max{8, 20} = 31.

		31 eд.

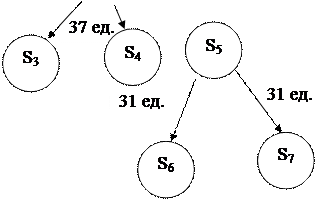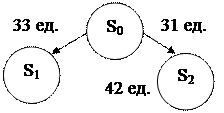
Рис. 2.5 – Результат ветвления шагов 1 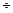7

ШАГ 9

S₈, z₃;

N (S₈) = { z₄ };

Y (S₈) = { z₀, z₂, z₁, z₅, z₃ };

t* (S₈) = τ₀ + t₀₂ + τ₂ + t₂₁ + τ₁ + t₁₅ + τ₅ + t₅₃ + τ₃ = 21;

T_оц (S₈) = t* (S₈) + max { t (L*₄) + max[0, T_H (z₄) – t* (S₈)]} =21 + max {3 + max[0, 28-21]} = 31.

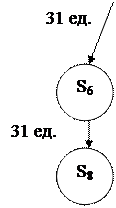Рис. 2.6 – Результат ветвления шагов 1 9

ШАГ 10

S₉, z₄;

N (S₉) = { z₆ };

Y (S₉) = { z₀, z₂, z₁, z₅, z₃, z₄ };

t* (S₉) = τ₀ + t₀₂ + τ₂ + t₂₁ + τ₁ + t₁₅ + τ₅ + t₅₃ + τ₃ + t₃₄ + τ₄ = 29;

T_оц (S₉) = t* (S₉) + max { t (L*₆) + max[0, T_H (z₆) – t* (S₉)]} =29 + max {3 + max[0, 31-29]} = 31.

Поскольку условие t* (S₉) ≤ min { T_оц (S_k) │ S_k 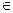S* } выполняется, то получено оптимальное решение.

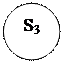
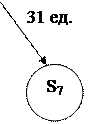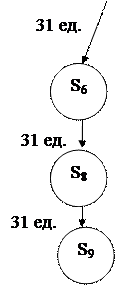Рис. 2.7 – Результат ветвления шагов 1 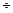10

Все полученные ранее данные сводятся в таблицу для определения оптимального варианта ветвления исходного графа (таблица 2.4)

Таблица 2.4

S	zi/i=Sk	N(Sk)	Y(Sk)	t*(Sk)	Tоц(Sk)
S0	z0	z1, z2	z0
S1	z1	z2	z0, z1
S2	z2	z3, z5, z1	z0, z2
S3	z3	z5, z1	z0, z2, z3
S4	z5	z1, z3	z0, z2, z5
S5	z1	z5, z3	z0, z2, z1
S6	z5	z3	z0, z2, z1, z5
S7	z3	z5, z4	z0, z2, z1, z3
S8	z3	z4	z0, z2, z1, z5, z3
S9	z4	z6	z0, z2, z1, z5, z3, z4

Окончательно дерево решений в соответствии с таблицей 2.4 имеет вид:

37 eд.

42 eд.

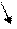
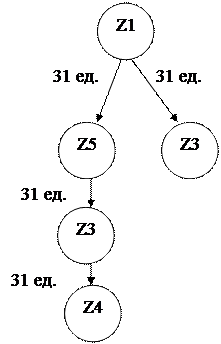Рис. 2.8 – Дерево решений (последовательность проведения проверок)

Таким образом оптимальному процессу проведения проверок соответствует следующая стратегия прохождения модулей и их порядков проведения z₁, z₂, z₅, z₃, z₄. При этом общее время контроля составит T_k = 31 ед.