Выбор порядка проведения операций контроля методом ветвей и границ

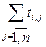Одной из задач организации процесса контроля является определение порядка проведения проверок для минимизации общего времени контроля Т_k. Исходными данными для этой задачи являются заданные в длительности t _I проведения n операций контроля z_i и времена перехода t_ij (задержек) от одной операции z_i к другой z_j, необходимые для коммутации цепей связи объект контроля - система контроля, ожидание окончания переходных процессов и т. д. При этом в общем случае времена задержек могут зависеть от порядка проведения проверок при фиксированной длительности операций ti. Таким образом минимизация Т_k заключается в определении порядка следования проверок, минимизирующее суммарное время переходов, причём после проведения всех операций необходим возврат к исходному состоянию объекта контроля (ОК), которое требуется для проведения первой операции, т. е. приведение ОК в исходное состояние. Поставленная задача сводится к классической задаче коммивояжера по минимизации времени обхода n городов, для которой разработан простой алгоритм. В рассматриваемой задаче исходными данными являются элементы t_ij матрицы Т, соответствующие дугам (i,j) графа возможных переходов между операциями.

Матрица Т обрабатывается по определенной схеме (и, следовательно, претерпевает изменения по отношению к первоначальному виду), что приводит к более простым вариантам, также задаваемым в виде матриц. Повторное применение стандартных приемов к каждому из этих вариантов продолжается до тех пор, пока не будет получено окончательное решение задачи. Грубо говоря, анализ каждой из матриц приводит к одной из трех возможностей:

Получению решения,когда решение находится непосредственно по исходной матрице, если задача достаточно проста.

Исключению матрицы из дальнейшего рассмотрения, когда можно показать, что из нее не следует решения задачи.

Ветвлению, состоящему в том, что решаемая задача приводится к рассмотрению двух вариантов менее громоздких задач.

Получаемое решение представляет собой сумму n слагаемых, каждое из которых определяется элементом матрицы Т в соответствии с принятым порядком:

t_[1],[2]+t_[2],[3]+…+t_[n-1],[n]+t_[n],[1]. (2.1)

Оптимальным решением будет перестановка, минимизирующая эту сумму.

Для некоторых пар i, j непосредственный переход от i к j может быть запрещён (например, если отсутствует дуга (i, j)): в этом случае элемент t_ij матрицы T полагается равным бесконечности. Тогда, если существует какое-то конечное решение задачи, то маршрут, соответствующий оптимальному решению, не содержит дуги (i, j).

В других случаях требуют, чтобы определенная дуга обязательно входила в маршрут, и разыскивают оптимальное решение при условии, чтобы маршрут непременно включал в себя дугу (i, j).

На каждом шаге описываемого алгоритма задача включает n операций, причём из n шагов переходов k могут быть уже установлены и нужно выбрать оптимальным образом оставшиеся n-k. Для всех возможных переходов необходимо задать значение Т_oц, представляющее собой оценку нижней границы всех возможных решений задачи, включая и оптимальное. Конечно, существуют тривиальные нижние границы, такие, например, как минимальный элемент матрицы Т или сумма минимальных элементов ее n строк. Трудность состоит в том, чтобы разумно построить эту нижнюю границу, стремясь сделать ее как можно больше.

Таким образом, матрица Т характеризуется оставшимся числом (n-k) неизвестных шагов маршрута и нижней границей Т_оц решений задачи. Кроме того, можно считать, что для оставшегося множества шагов известно по крайней мере одно решение задачи (например, перестановка 1, 2, …, n есть решение), и пусть Т будет лучшее из них, причем сначала Т может быть бесконечным. Теперь матрица претерпевает дальнейшие изменения в зависимости от следующих возможностей:

а) Если n-k =2, то осталось не более двух шагов маршрута и решение находится сразу. Если его значение меньше Т, то Т принимается равным этому новому значению и считается лучшим из известных решений.

b) Если Т_oц больше или равно Т, то матрица исключается, поскольку представленные в ней маршруты не приводят к решениям, лучшим, чем уже известное.

с) Если не имеет места ни одна из перечисленных ситуаций, то вместо исходной матрицы составляются две. Происходит как бы ветвление исходной траектории в двух направлениях и каждому из направлений соответствует своя матрица:

1) в одной из них выбирается переход от i к j, в результате чего нижняя граница может возрасти;

2) в другой запрещается переход из i в j (элемент t_ij полагают равным 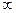), в результате чего нижняя граница решений несомненно возрастет.

Таким образом, получаемые матрицы характеризуются возрастающей нижней границей и (или) большим числом установленных шагов. Кроме того, для каждой последующей матрицы число возможных траекторий меньше, чем для предыдущей и в конце концов достигается такое состояние, когда маршрут определен полностью.

Ситуации, когда решение получается сразу или матрица исключается, очевидны; особенность данного алгоритма в ветвлении. Суть ветвления составляют понятия приведения и выбора. Приведение преследует цель получения по меньшей мере по одному нулю в каждой строке и каждом столбце исходной матрицы Т. Так как каждое решение задачи включает один и только один элемент из каждой строки или столбца матрицы Т, то вычитание или добавление постоянной к каждому элементу ее столбца или строки в одинаковой степени изменяет все решения и не приводит смещению оптимума.

Отнимем постоянную h от каждого элемента строки или столбца матрицы Т. Пусть получаемая в результате этого матрица будет 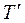. Тогда оптимальное решение, найденное из 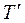, оптимально и для T, т.е. для обеих матриц перестановка, минимизирующая порядок следования операций, имеет один и тот же вид. В качестве нижней границы решений, получаемых на 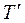, можно выбратьT^/_оц= h Вычитание можно продолжать до тех пор, пока каждый столбец или строка не будут содержать по крайней мере одного нуля (т.е. до величины минимального элемента в каждой строке или каждом столбце). Сумма всех констант приведения определяет нижнюю границу Т _оц для исходной задачи. Определяется, что матрица Т является приведенной, если она не допускает дальнейшего приведения. В этом случае отыскание возможных вариантов маршрута связано в дальнейшем с изучением какого-либо перехода, скажем, из i в j. В результате вместо исходной матрицы рассматривают две:

матрицу T_ij, связанную в отысканием лучшего из всех решений, даваемых матрицей N и включающих дугу (i, j);

матрицу T_n(i,j), связанную с выбором лучшего из всех решений, не включающих дугу (i, j).

После того как фиксирован переход из i в j, нужно исключить переходы от операций z_i во все другие операции, кроме z_j, и переходы в j от всех других операций, кроме i, полагая все элементы строки i и столбца j, за исключением t_ij, равными бесконечности. Нужно также запретить в последующем выбор дуги (i, j), полагая t_ji = 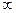. Это вызвано тем, что выполнение всех операций при заключительной операции приводящей, объект в исходное состояние не может включать в себя одновременно дуги (i, j) и (j,i). Так как эти запрещения могут привести к устранению ряда нулей в матрице T, то не исключена возможность дальнейшего приведения T и в результате этого получения новой большей нижней границы для решений, связанных с матрицей t_ij.

В матрице T_n(i,j) запрещается переход из i в j, т.е. полагается t_ij = 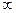. В этом случае также не исключена возможность дальнейшего приведения матрицы и вызванного этим возрастания нижней границы для решений, получаемых из T_n(ij). Выбор дуги (i, j) должен быть таким, чтобы максимально увеличить нижнюю границу для T_n(ij), что, возможно, позволит исключить из рассмотрения ряд траекторий без дальнейшего ветвления. Чтобы достигнуть этого, просматриваются все возможные пары (i, j) в матрице T_n(ij) и выбор осуществляется таким образом, чтобы сумма двух последовательных приводящих констант была максимальной. Очевидно, что в первую очередь должны запрещаться дуги (i, j), которым соответствуют нулевые элементы матрицы T, поскольку выбор дуг с нулевыми элементами не способствуют дальнейшему приведению T_n(ij).

В качестве примера рассматривается решение задачи коммивояжера в приложении к выбору последовательности контрольных операций с исходной матрицей Т переходов (задержек) между операциями:

.

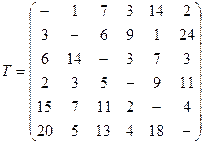
Эта матрица может быть приведена к матрице

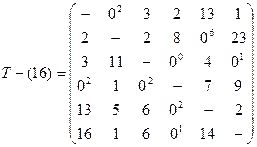
последовательным вычитанием из ее столбцов и строк минимальных элементов, общая сумма которых равна 16. прочерки в матрицах соответствуют запрещенным переходам.

На первом шаге таблица представляет собой матрицу T-(16), где 16 означает, что любое решение исходной задачи, получаемое по матрице T-(16), не может иметь значение, меньше 16. Одно решение известно, так как последовательность 1-2-3-4-5-6, безусловно, является возможным решением. Поэтому T_z =43.

Степень нулевых элементов T-(16) означает сумму констант приведения, которая достигается запрещением соответствующего перехода. Максимальное из этих чисел равно 6 (для элемента t ₂₅), поэтому дальнейшее преобразование таблицы связано с этим элементом. Здесь возможны два варианта, представленных ниже.

Матрица второго шага (Т =43)

,

.

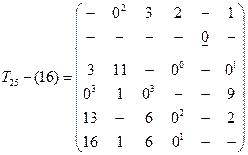
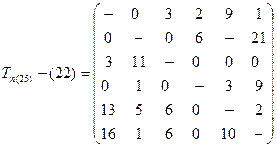
Следовательно, на втором шаге таблица содержит две матрицы: 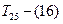и 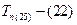. Видно, что T_n(25) приводится дальше с суммой констант приведения, равной 6 (4 по 5-му столбцу и 2 по 2-й строке), в результате чего нижняя граница возрастает до 22. в матрице T₂₅ элемент t₂₅ подчеркнут для обозначения того, что он обязательно должен войти в решение. Остальные переходы по 2-й строке и 5-му столбцу запрещены. Заметим, что переход, определяемый элементом t₅₂, также запрещен. Это обусловлено тем, что решение, получаемое из T₂₅, содержит элемент t₂₅, и оно не может содержать элемента t₅₂, иначе произойдет повторное выполнение одной из операций, прежде чем будет завершена процедура. В обоих вариантах, представленных в таблице, нижняя граница меньше T_z, и для полного построения процедуры остается найти более чем две операции. Кроме того, ни один из этих вариантов ни приводит к решению, ни может быть отвергнут. Поэтому каждый из них должен быть исследован дополнительно.

Наиболее перспективным является исследование матрицы T₂₅, поскольку она содержит то же самое число выполненных операций, но имеет меньшее значение T_оц. Здесь также значение степени каждого нуля определяет направление поиска. Выбирается элемент s₄₁ и получаем матрицы T_25,41-(19) и T_25,n(41)-(19). Матрица T_n(25)-(22) остается в том же виде, какой она имела на втором шаге.

Матрица третьего шага (Т =43)

,

.

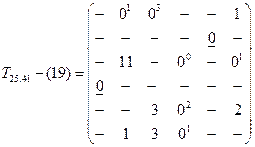
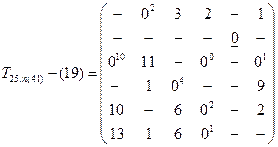
На четвертом шаге в матрице T_25,41 вычеркивается не только элемент t₃₁, но и t₃₄. Это вызвано необходимостью исключить цикл 4-1-3-4, поскольку переходы 4-1 и 1-3 уже включены в маршрут.

Матрица четвертого шага (Т =43)

,

.

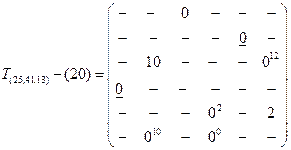
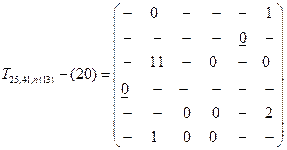
Продолжая подобную процедуру дальше, на пятом шаге формируется матрица T_25,41,13,36-(20), приводящая к решению задачи, поскольку остается установить только два перехода для завершения маршрута. Пять переходов должны определить минимум пять операций; остается только одина операция и только одна возможность включения её в маршрут, чтобы удовлетворить заданным условиям.

Другие результаты для работ с одной операцией

Матрица пятого шага (T = 43)

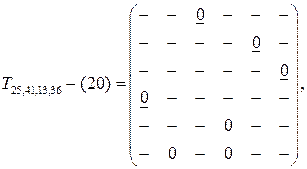
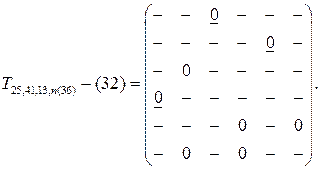
В рассматриваемом случае пять переходов приводят к двум несвязанным друг с другом участкам маршрута 2 – 5 и 4 – 1 – 3 – 6. соответствующий выбор элементов в последний матрице позволяет соединить эти участки в один маршрут. Такими элементами является T₅₄ и T₆₂ (другой выбор просто отсутствует). Окончательный маршрут с длиной 20 имеет вид 6-2-5-4-1-3. Это новое значение T=20 позволяет отвергать сразу три из оставшихся вариантов решения. В результате остается только вариант, содержащийся в матрице T_25,n(41) – (19). Здесь еще можно рассчитывать на получение решения со значением, меньшим 20. Преобразование этой матрицы по элементу t₃₁ приводит к матрицам T_25,n(41),31-(20) и T_25,n(41),31-(29). Однако варианты содержащиеся в матрицах T_25,n(41),31-(20) и T_25,n(41),n31-(29), отвергаются, больше вариантов не остается, и задача решена.

Матрица шестого шага

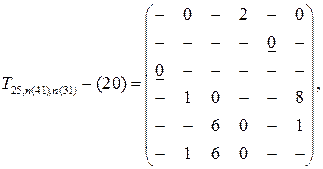
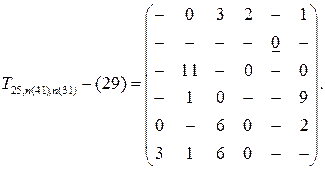
Процесс поиска вариантов решения удобно представить в виде дерева (рис. 2.1.) Каждый узел на рис. 2.1 соответствует одному из вариантов, содержащихся в таблицах.

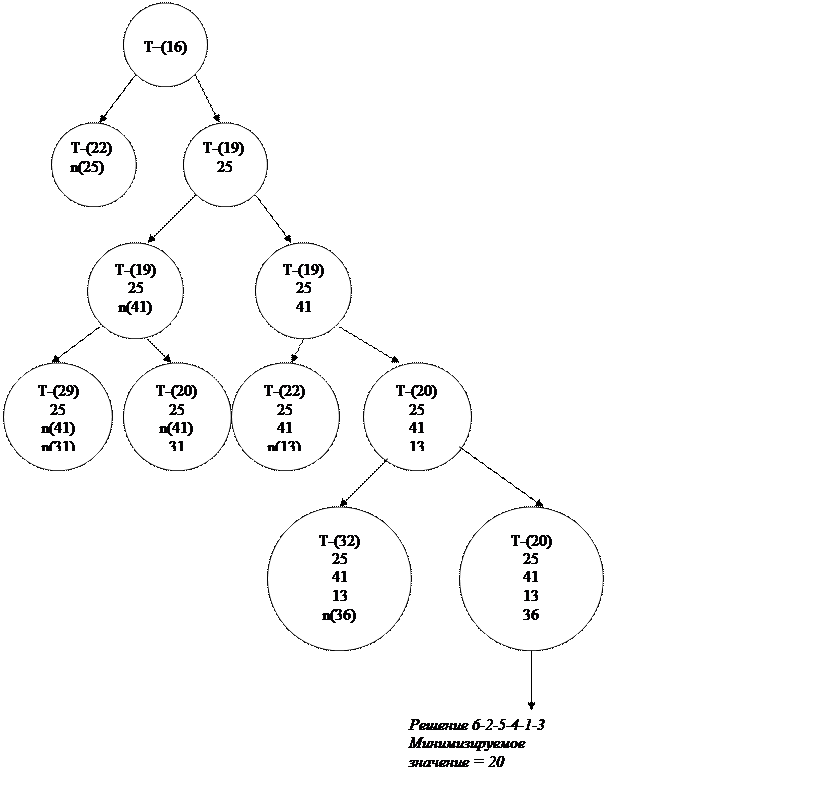
Рис. 2.1 Дерево решений

Время затрачиваемое на вычисления по данному алгоритму, с увеличением числа операций возрастает экспоненциально. Как правило, добавление 10 операций увеличивает время вычислений в 10 раз». Подобное возрастание времени вычисления с увеличением числа операций присуще любому из известных в настоящее время алгоритмов решения подобной задачи.