Выбор порядка проведения проверок методом динамического программирования

Алгоритм с использованием этого метода является, по видимому, более общим чем метод ветвей и границ и применим к более широкому классу задач упорядочения. Однако трудности, связанные с объёмом и временем вычислений при применении этого алгоритма, появляются для задач меньшего объёма данных чем при решении методом ветвей и границ.

Алгоритм состоит в следующем. Все множество контрольных операций разбивается на четыре непересекающихся подмножества:

1) {z₀} – множество, состоящее только из одной исходной операции;

2) {z_i} – множество, состоящее только из одной операции (не исходной);

3) {Z_k} – множество, состоящее из k операций, за исключением z₀ и z_i;

4) {Z_n-k-2} – множество оставшихся (n – k - 2) операций.

Пусть, далее, известен оптимальный порядок выполнения операций, начинающийся и заканчивающийся операций z₀. Тогда можно выбрать операции z₀ и подмножество { Z_k }, состоящее из k операций, таким образом, что этот оптимальный маршрут начинается в z₀ и происходит через множество { Z_n-k-2 }, затем через z_i, после чего, выполнив множество операций {Z _r }, завершается выполнением z_i.

Теперь рассмотрим только ту часть перехода, которая связывает z_i и z₀ с промежуточным выполнением операций { Z_k }. Для этого интервала известен наикратчайший путь. Если бы это было не так, то, не изменяя части интервала до операции z_i, можно было бы найти лучший путь его завершения и, следовательно, наикратчайший маршрут целиком. Но это невозможно, поскольку противоречит исходному предложению, что оптимальный маршрут известен.

Пусть f (z_i; {Z_k}) – длительность наименьшего перехода от z_i к z₀ с промежуточным выполнением операций множества { Z_k }. Затем, что при k=0

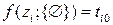
есть элемент матрицы T. Если k = n – 1 и z_i совпадает с началом движения, то f (z₀; {Z_n-1}) является длительностью оптимального маршрута исходной задачи. Идея метода динамического программирования состоит в том, чтобы, начиная с k = 0, шаг за шагом увеличивать k. При этом, начав с z₀, маршрут выполняется в обратном порядке до z₀ и тем самым находится оптимальное решение.

Для рассматриваемой задачи основное функциональное уравнения динамического программирования имеет вид

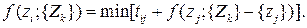(2.1)

Это уравнение показывает, что для того, чтобы найти лучший маршрут, начинающийся с z_i и завершающийся выполнением z₀, с промежуточным выполнением k операций, нужно выбрать наикратчайший из k возможных путей, начинающихся переходом от z_i в одну из k операций и затем проходящий кротчайшим образом к z₀ с промежуточным выполнением (k-1) других. Любой из этих k вариантов, в свою очередь, представляет собой наикратчайший из (k- 1) возможных маршрутов в соответствии с приведенным ранее уравнением. В конце концов достигается точка, в которой правая часть уравнения представляет собой просто элемент T.

В качестве примера рассмотрим решение задачи для пяти операций, и пусть пятая операция принимается за начало маршрута. Тогда

f (z₅;{ z₁, z₂, z₃, z₄ }) представляет собой длительность кратчайшего маршрута и любая очередность выполнения операций, приводящая к этой длительности маршрута, является оптимальной. На нулевом шаге ищется решение для четырех вариантов при k = 0:

0-й шаг (k = 0)

4 варианта

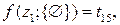
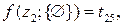
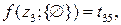
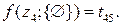
На первом шаге решения при k = 1 выражаются через известные решения при k = 0:

1-й шаг (k = 1)

12 вариантов

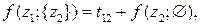
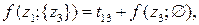
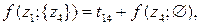
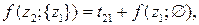
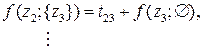
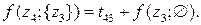
На втором шаге решения при k = 2 выражаются через известные решения при k = 1

2-й шаг (k = 2)

12 вариантов

………………………………………………………

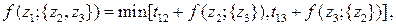
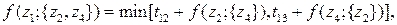
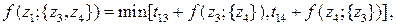
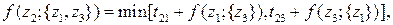
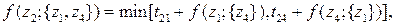
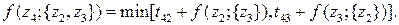
На втором шаге используются каждое из решений, полученных на первом шаге. При этом, если сделан выбор в правой части, то выбранный член должен быть зафиксирован, так как он соответствует фактическому направлению переходов. Например, если

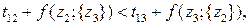
то

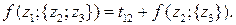
Таким образом, всякий раз, попав в z₁, чтобы пройти множество, состоящее из z₂, z₃ и z₄, нужно сначала перейти в z₂, затем в z₃, после чего вернуться в z₅, затратив время f (z₁;{ z₂, z₃ }).

На третьем шаге используюется каждое из решений второго шага.

3-й шаг (k = 3)

4 варианта

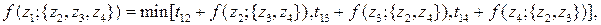
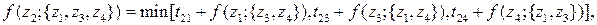
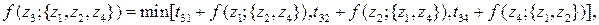
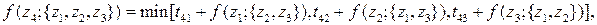
Наконец, на четвертом шаге получается решение исходной задачи.

4-й шаг (k = 4)

1 вариант

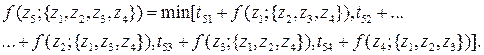
Таким образом операции необходимо выполнять в определённом порядке.

Чтобы оценить объем вычислительной работы, связанной с описываемым методом, подсчитывается число вариантов на каждом шаге. В общем приходится просматривать 33 варианта и проделать 108 арифметических операций с данными, содержащимися в матрице T или полученными на предыдущем шаге. Поиск решения, основанный на методе полного перебора всех вариантов, содержит (n - 1)! вариантов, т.е. 24 варианта. Каждый из этих вариантов требует пяти арифметических операций на основании данных матрицы T, т.е. в общем требуется 120 арифметических операций. С возрастанием числа операций преимущества, даваемые методом динамического программирования, становится еще более ощутимыми.