Алгоритм метода ветвей и границ для решения одномерных задач целочисленного программирования

В математическом анализе рассматривается класс задач, объединенных понятием задачи целочисленного программирования. В общем виде они могут быть сформулированы как максимизация некоторого выражения в условиях ограничений.

Рассмотрим следующую задачу целочисленного программирования. Тре­буется максимизировать выражение

(1.1)

при ограничениях

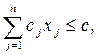
(1.2)

x_j 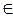{0;1}, j =1,…,n, (1.3)

причем p_j ≥0, c_j ≥0.

Решение задачи может быть получено с помощью метода ветвей и границ.

Метод ветвей и границ использует последовательно-параллельную схему построения дерева возможных вариантов. Первоначально ищут допустимый план и для каждого возможного варианта определяют верхнюю границу целевой функции. Ветви дерева возможных вариантов, для которых верх­няя граница ниже приближенного решения, из дальнейшего рассмотрения исключают.

Эффективность вычислительных алгоритмов зависит от точности и простоты способа определения верхней границы возможных решений и точности определения приближенного решения. Чем точнее способ опреде­ления верхней границы целевой функции, тем больше бесперспективных ветвей отсекается в процессе оптимизации. Однако увеличение точности расчета верхних границ связано с возрастанием объема вычислений. Напри­мер, если для оценки верхней границы использовать симплекс-метод, то результат будет достаточно точным, но потребует большого объема вы­числительной работы.

Рассмотрим алгоритм решения задачи (1.1) — (1.3) методом ветвей и границ с простым и эффективным способом оценки верхней границы целевой функции.

Множество U переменных x_j рассматривается как три множества.

S -множество фиксирован­ных переменных, вошедших в допустимое решение; E_s — множество за­висимых переменных, которые не могут быть включены в множество S, так как для них выполняется неравенство

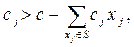
G_S — множество свободных переменных, из которых производится выбор для включения в S очередной переменной.

Обозначим h_1j = p_j/c_j и допустим, что x_j 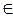S (j= 1,..., k < п), вычисляется указанное отношение и параметры номеруются (ранжируются) в соответствии с ранжировкой h_1,k+1 ≥h_1,k+2≥...≥h_1l, l≤n, (1.4)

(1.5)

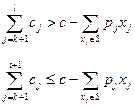
(1.6)

Условия (1.5), (1.6) означают, что в множество S без нарушения нера­венства (1.2) можно дополнительно ввести элементы х_к+1, х_{к +2},..., х_l-1. При введении в множество S элементов х_к+1, х_{к +2},..., х_l неравенство (1.2) не выполняется.

L'S

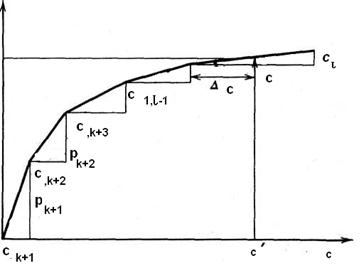
Рис. 1.1 Кусочно-линейная функция

Для определения верхней границы решения может быть использовано
выражение

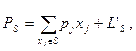(1.7)

где

(1.8)

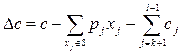(1.9)

Из условий (1.1)-(1.3) следует, что L'_s не меньше максимального значения величины

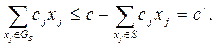при ограничениях

Поясним процесс определения L'_S графиком (рис. 1.1). Строим кусочнолинейную функцию L(с) с убывающим значением градиента h. Вычисля­ем с'₁ и по графику находим L'_S.

Выбор очередной переменной для включения в множество S производит­ся с помощью условия

(1.10)

Для выбранной переменной х_r определяются величины Р_S(x_r) и Р_S(x_r), т.е. в S включается х_r = 1 или х_r = 0.

Если в процессе решения окажется, что в множестве G_S нет элементов, которые могут быть введены в множество S без нарушения ограничения (1.5), то полученное решение 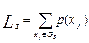принимается в качестве первого приближенного решения L₀.

Все вершины дерева возможных вариантов, для которых выполняются условия Q_S ≤ L₀ из дальнейшего рассмотрения исключаются.

Из оставшихся ветвей выбирается ветвь с максимальным значением Р_S, и процесс поиска оптимального варианта продолжается. Если в процессе решения будет найдено 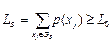, то полученное решение принимается в качестве нового приближенного результата. Вычислительная процедура заканчивается, если для всех оставшихся ветвей выполняется условие Р_S ≤ L₀.