Дифференцирование оригинала

Если функция f (t) является оригиналом с показателем роста , причем , и существует (по крайней мере, при ) производная , являющаяся оригиналом, то

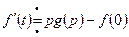, (2.8)

где есть правое предельное значение, то есть

.

Предполагая 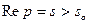и последовательно используя определение изображения и формулу интегрирования по частям, будем иметь

, (2.9)

если двойная подстановка и несобственный интеграл в правой части существуют.

Так как при , ибо

то , .

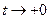
Тогда равенство (2.9) может быть переписано так: .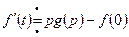

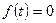Особенно важный частный случай правила дифференцирования оригинала (2.8) мы имеем, когда функция f (t) непрерывна при t= 0. Тогда , так как при 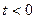по определению оригинала, следовательно, левое предельное значение , а в силу непрерывности правое предельное значение должно быть равно левому.

В этом случае формула (2.8) приобретает вид

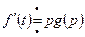(2.10)

Правило дифференцирования оригинала распространяется на старшие производные следующим образом: Если функция f (t) является оригиналом с показателем роста s_o, причем , и существуют (по крайней мере при ) производные , являющиеся оригиналами, то

, (2.11)

где , ,…, (0) есть правые предельные значения функции 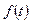и ее производных в точке .

В самом деле, повторное применение формулы (2.8), возможность которого обеспечивается условиями, последовательно дает:

;

;

,

………………………………………………………

.

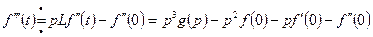Если 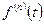непрерывна при , то 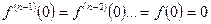и формула (2.11) приобретает вид 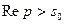. (2.12)

Правило дифференцирования оригинала является особенно важным свойством преобразования Лапласа, в значительной мере обеспечившим его пригодность для многочисленных приложений. Формулы (2.10) и (2.12) показывают, что операции дифференцирования оригинала соответствует более простая операция умножения изображения на степени комплексного переменного. То обстоятельство, что применение формул (2.8) и (2.11) связано с учетом предельных значений оригинала и его производных, хотя и несколько усложняет выкладки, но, в конечном счете, выгодно, так как обеспечивает получение сразу решения дифференциального уравнения, удовлетворяющего начальным условиям (это выяснится в дальнейшем).

Пример 5. Так как 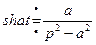и , то по формуле (2.10) имеем

, .