Указания к выполнению контрольных заданий 3 страница

Для того, чтобы получить интервальную оценку, определим величину предельной ошибки прогноза.

Она рассчитывается по формуле:

,

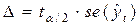где 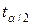- табличное значение t - критерия Стьюдента для уровня значимости α и числа степеней свободы (k = n - 2);

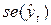- стандартная ошибка точечного прогноза, которая, в свою очередь, рассчитывается по формуле:

,

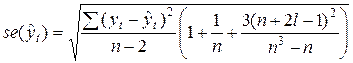где 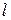- длина периода упреждения (срок прогноза).

Расчеты проведем в рабочей таблице.

	t
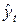
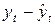
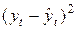
1994	-2,5	30	30,0476	-0,0476	0,0023
1995	-1,5	35	34,7619	0,2381	0,0567
1996	-0,5	39	39,4762	-0,4762	0,2268
1997	0,5	44	44,1905	-0,1905	0,0363
1998	1,5	50	48,9048	1,0952	1,1995
1999	2,5	53	53,6190	-0,6190	0,3832
Суммы	0,00	251	197,3810	0,0000	1,9048

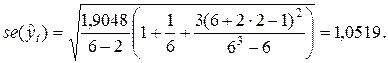
Табличное значение t - критерия Стьюдента для уровня значимости α = 0,05 и числа степеней свободы k = 6 – 2 = 4 составляет 2,78, т.е. 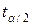=2,78.

Отсюда,

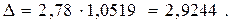
Таким образом,

;

.

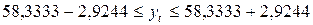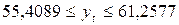С вероятностью 0,95 можно ожидать, что в 2000 году расходы семьи на товар "А" будут находиться в пределах от 55,4089 до 61,2577 руб.

Обратите внимание на то, что приведенные формулы верны только для уравнения парной регрессии, линейной по параметрам.

Задача 4.

Рассмотрим методику решения задачи на примере:

Имеются следующие данные о величине дохода в расчете на одного члена семьи в процентах к 1994 году и о расходах семьи на товар "А" в 1994-1999 гг.:

Годы	1994	1995	1996	1997	1998	1999
Расходы на товар "А", руб.	30	35	39	44	50	53
Доход на одного члена семьи в процентах к 1994 году, %	100	103	105	109	115	118

Пункт 1. Определение функциональной формы трендового уравнения регрессии описано в пункте 2 к задаче 3.

Пункты 2-3. При измерении корреляции между двумя временными рядами следует учитывать возможность наличия ложной корреляции, обусловленной простым сопутствием временных рядов. Для того чтобы устранить ложную корреляцию, следует определять степень тесноты связи не самих уровней временных рядов, а их последовательных (первых или вторых) разностей или отклонений от трендов (если последние не содержат тенденции).

Сделайте вывод о наличии или отсутствии ложной корреляции при разных способах измерения связи между исследуемыми временными рядами, поясните причины существования ложной корреляции.

По данным примера рассчитаем коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи по исходным уровням ряда:

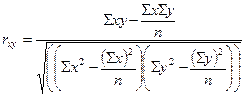
Заметим, что расчет может быть осуществлен и по другим формулам.

Промежуточные расчеты проведем в рабочей таблице.

Годы	y	x	xy	y2	x2
1994	30	100	3000	900	10000
1995	35	103	3605	1225	10609
1996	39	105	4095	1521	11025
1997	44	109	4796	1936	11881
1998	50	115	5750	2500	13225
1999	53	118	6254	2809	13924
Суммы	251	650	27500	10891	70664

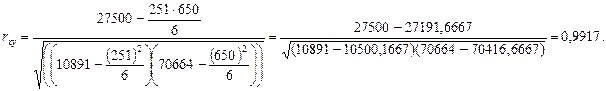
Близкое к единице значение коэффициента корреляции свидетельствует о тесной прямой связи между расходами на товар "А" и доходом на одного члена семьи.

Однако, учитывая, что расчет был произведен по уровням временного ряда, корреляция между изучаемыми признаками может быть вызвана простым сопутствием явлений во времени.

Для того, чтобы исключить тенденцию, рассчитаем коэффициент корреляции по первым разностям.

Промежуточные расчеты проведем в рабочей таблице.

Годы	y	x	Δy	Δx	ΔxΔy	Δy2	Δx2
1994	30	100
1995	35	103	5	3	15	25	9
1996	39	105	4	2	8	16	4
1997	44	109	5	4	20	25	16
1998	50	115	6	6	36	36	36
1999	53	118	3	3	9	9	9
Суммы	251	650	23	18	88	111	74

.

.

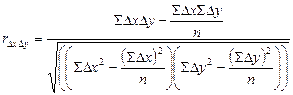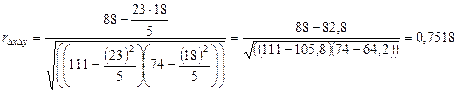Коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи, рассчитанный по первым разностям, показывает не столь тесную связь, как коэффициент, рассчитанный по уровням ряда динамики.

Расчет коэффициента корреляции по первым разностям позволяет устранить тенденцию, зависимость между x и y, обусловленную сопутствием рядов во времени.

Рассчитаем коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи по отклонениям от тренда.

Прежде, чем рассчитывать отклонения от тренда, определим функциональную форму трендовых уравнений регрессии расходов на товар "А" и дохода на одного члена семьи.

Слабая колеблемость первых разностей (цепных абсолютных приростов) позволяет говорить о линейной форме обеих моделей.

Трендовое линейное уравнение регрессии расходов на товар "А" имеет вид (расчеты см. в методических указаниях к решению задачи 3):

.

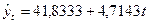Аналогично рассчитаем параметры трендового линейного уравнения регрессии доходов в расчете на одного члена семьи:

Годы	t	x	xt	t2
1994	-2,50	100	-250	6,25
1995	-1,5	103	-154,5	2,25
1996	-0,5	105	-52,5	0,25
1997	0,5	109	54,5	0,25
1998	1,5	115	172,5	2,25
1999	2,5	118	295	6,25
Суммы	0	650	65	17,5

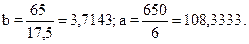
Таким образом, трендовое линейное уравнение регрессии имеет вид:

.

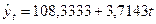Перейдем к расчету коэффициента корреляции по отклонению от тренда согласно формуле:

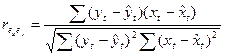
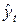
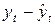
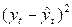
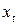
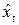
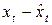
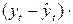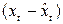
1994	30	30,0476	-0,0476	0,0023	100	99,0476	0,9524	0,9070	-0,04535
1995	35	34,7619	0,2381	0,0567	103	102,7619	0,2381	0,0567	0,056689
1996	39	39,4762	-0,4762	0,2268	105	106,4762	-1,4762	2,1791	0,702948
1997	44	44,1905	-0,1905	0,0363	109	110,1905	-1,1905	1,4172	0,226757
1998	50	48,9048	1,0952	1,1995	115	113,9048	1,0952	1,1995	1,199546
1999	53	53,6190	-0,6190	0,3832	118	117,6190	0,3810	0,1451	-0,23583
Суммы	251	197,3810	0,0000	1,9048	650	532,3810	0,0000	5,90476	1,90476

.

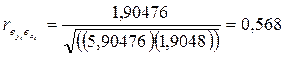Величина этого коэффициента корреляции еще более убедительно свидетельствует о сопутствии рядов во времени.

Пункт 4. По аналогии с коэффициентами корреляции параметры уравнения регрессии по временным рядам определяют также не по исходным их уровням, а по последовательным разностям, либо отклонениям от тренда.

Обратите внимание на интерпретацию параметров, полученных уравнений регрессии:

- если уравнение регрессии построено по первым разностям, то коэффициент регрессии b характеризует изменение прироста результативного признака при изменении прироста факторного признака на единицу.

Сделайте общий вывод о наличии и тесноте причинно-следственной связи между изучаемыми временными рядами, укажите ее направление.

Определим параметры уравнения парной линейной регрессии по первым разностям.

Расчет осуществляется обычным методом наименьших квадратов:

Годы	y	x	Δy	Δx	ΔxΔy	Δy2	Δx2
1994	30	100
1995	35	103	5	3	15	25	9
1996	39	105	4	2	8	16	4
1997	44	109	5	4	20	25	16
1998	50	115	6	6	36	36	36
1999	53	118	3	3	9	9	9
Суммы	251	650	23	18	88	111	74

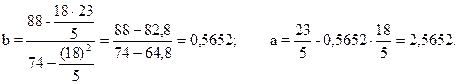
Отсюда, модель имеет вид:

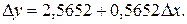
Коэффициент регрессии b = 0,5652 означает, что с изменением прироста душевого дохода на 1 процентный пункт расходы на товар "А" изменяются с ускорением, равным 0,5652 руб.

Задача 5 посвящена методике выявления сезонной компоненты в рядах динамики, построению моделей с аддитивной и мультипликативной сезонными компонентами и прогнозированию по этим моделям.

Для выявления тренда и наличия сезонной компоненты постройте график ряда динамики (пункт 1). При построении графика ряда динамики по оси абсцисс откладываются временные промежутки, а по оси ординат – уровни ряда.

Приступая к выполнению пункта 2, изучите вопрос об особенностях анализа сезонных колебаний.

Сезонная колеблемость в рядах динамики может иметь аддитивный и мультипликативный характер.

Если сезонная вариация постоянна в различных временных периодах, то для анализа временного ряда подходит модель с аддитивной компонентой.

Если сезонная вариация не является константой, например, увеличивается с возрастанием значений тренда, то для анализа лучше подходит модель с мультипликативной компонентой, в которой значения сезонной компоненты представляют собой определенную долю трендового значения.

В зависимости от особенностей сезонной вариации сделайте выбор между моделями с аддитивной и мультипликативной компонентами.

Каждой из этих моделей соответствуют различные методы расчета сезонной компоненты тренда, использующие сочетание методов скользящего среднего и линейной регрессии.

Следует помнить, что поскольку сезонные колебания характеризуются относительно небольшими временными интервалами, то прогнозирование по моделям с сезонной компонентой – также краткосрочное.

Модель с аддитивной компонентой. Если сезонная компонента переменной А – постоянна, модель фактических значений переменной А можно представить следующим образом:

Фактическое значение =

= Трендовое значение + Сезонная вариация + Ошибка,

то есть:

A = T + S + E.

Модель с мультипликативной компонентой. Если значение сезонной компоненты переменной А, не является константой, а представляет собой определенную долю трендового значения, т.е. значения сезонной компоненты увеличиваются с возрастанием значений тренда, модель фактических значений переменной А можно представить следующим образом:

Фактическое значение =

= Трендовое значение Сезонная вариация Ошибка,

т.е.

А = T S E.

В моделях, как с аддитивной, так и с мультипликативной компонентой общая процедура анализа примерно одинакова:

Шаг 1. Расчет значений сезонной компоненты.

Шаг 2. Десезонализация данных. Для модели с аддитивной компонентой он состоит в вычитании сезонной компоненты из фактических значений. Для модели с мультипликативной компонентой – в расчете отношений между фактическими значениями и сезонной составляющей. Расчет тренда на основе полученных десезонализированных данных.

Шаг 3. Расчет ошибок как разности между фактическими и трендовыми значениями. В мультипликативной модели можно рассчитать ошибки еще и как отношение между фактическими и трендовыми значениями.

Шаг 4. Расчет среднего линейного отклонения или среднеквадратической ошибки для обоснования соответствия модели исходным данным или для выбора из множества моделей наилучшей.

Для того чтобы элиминировать влияние сезонной компоненты ( пункт 3 ) воспользуйтесь методом скользящей средней. Если сезон состоит из 4-х кварталов (год), следует провести сглаживание по 4-м точкам, если сезон состоит из 7-и дней (неделя) следует провести сглаживание по 7-и точкам и т.д.

Значения уровней ряда, сглаженные по четному числу точек необходимо центрировать.

Множество скользящих средних представляет наилучшую оценку искомого тренда.

Процедуры сглаживания и центрирования одинаковы при построении моделей с аддитивной и мультипликативной компонентами.

Полученные значения тренда используйте для нахождения оценок сезонной компоненты.

Для модели с аддитивной компонентой:

A – T = S + E.

Для модели с мультипликативной компонентой:

А/Т= S E.

Найдите средние значения сезонных оценок для каждого года (недели и т.п.). Эта процедура позволяет уменьшить некоторые значения ошибок.

Скорректируйте средние значения.

Для модели с аддитивной компонентой корректировка состоит в увеличении или уменьшении средних значений на одно и то же число таким образом, чтобы их общая сумма была равна нулю. Это необходимо для того, чтобы усреднить значения сезонной компоненты в целом за период. Обычно корректирующий фактор рассчитывается путем деления суммы оценок сезонных компонент на число сезонов.

В мультипликативной модели значения сезонной компоненты - это относительные величины. Поэтому необходимо, чтобы их сумма была равна числу сезонов, а не нулю, как в случае с аддитивной моделью. Если это не так, произведите корректировку значений сезонной компоненты.

Шаг 2 состоит в десезонализации исходных данных ( пункт 4 ).

В модели с аддитивной компонентой она заключается в вычитании соответствующих значений сезонной компоненты из фактических значений данных за каждый квартал (день и т.п.), то есть:

A – S = T + E.

В модели с мультипликативной компонентой процедура десезонализации осуществляется по формуле:

А/S= T E.

Новые оценки тренда, которые все еще содержат ошибку, используйте для построения модели основного тренда. Нанесите эти значения на исходную диаграмму, сделайте вывод о наличии тренда.

Пункт 5 посвящен подбору уравнения тренда с аддитивной или мультипликативной компонентой. При этом выбор функциональной формы тренда осуществляется, исходя из общих принципов, изложенных в пункте 2 к задаче 3.

Предположим, например, что тренд – линейный.

Уравнение линейного тренда имеет вид:

,

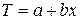где х – порядковый номер квартала,

а и b – параметры уравнения парной регрессии.

Поскольку предполагается, что тренд имеет линейный характер, то значения параметров линии, аппроксимирующей тренд, найдите методом наименьших квадратов:

где y = T + E,

,

.

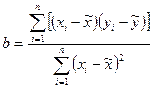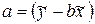Пункт 6 заключается врасчете ошибки (Е), среднего абсолютного отклонения (MAD) и среднеквадратической ошибки (MSE) модели.

Расчет этих показателей соответствует шагу 3 алгоритма и предшествует составлению прогноза.

Осуществите расчет ошибок или остатка.

В аддитивной модели он осуществляется по формуле:

Е = А - S - Т.

В мультипликативной:

Е = А/(Т S)

или

Е = А - (Т S).

Найдите меру соответствия модели исходным данным, т.е. определите ту часть колеблемости уровней ряда, которую невозможно объяснить с помощью построенной модели.

Для этого используйте среднее абсолютное отклонение (mean absolute deviation - MAD) и среднеквадратическую ошибку (mean square error - MCE):

;

.

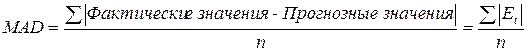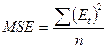Целесообразно использовать обе меры, так как последняя из них резко возрастает при наличии высоких ошибок.

Пункт 7 состоит в прогнозировании на основании полученных моделей.

Прогнозные значения по модели с аддитивной компонентой рассчитайте по формуле:

F = T + S.

В модели с мультипликативной компонентой используйте следующий алгоритм:

F= Т S.

Не следует забывать: чем более отдаленным является период упреждения, тем меньшей оказывается обоснованность прогноза.

Рассмотрим практическую реализацию методики решения задачи для модели с аддитивной компонентой.

В таблице 1 представлено количество продукции, проданной компанией FORA LTD в течение последних 13 кварталов.

Таблица 1. Количество продукции, проданной в течение последних 13 кварталов

ДАТА	Количество проданной продукции, тыс. шт.
Январь - март 1996	239
Апрель – июнь	201
Июль – сентябрь	182
Октябрь – декабрь	297
Январь - март 1997	324
Апрель – июнь	278
Июль – сентябрь	257
Октябрь – декабрь	384
Январь - март 1998	401
Апрель – июнь	360
Июль – сентябрь	335
Октябрь – декабрь	462
Январь - март 1999	481

Построим график, позволяющий сделать выводы о типе модели:

Стабильность сезонной компоненты указывает на то, что модель с аддитивной компонентой подходит для анализа этого временного ряда. То есть фактические объемы продаж можно выразить следующим образом:

A = T + S + E

Для того чтобы элиминировать влияние сезонной компоненты воспользуемся методом скользящей средней, которую рассчитаем с интервалом в три месяца. Этот расчет и все последующие проведем в таблице 2.

Таблица 2. Расчет по 4 точкам центрированных скользящих средних значений тренда для модели A – T = S + E