 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Прогнозирование по модели с мультипликативной компонентой
|
|
При составлении прогнозов по любой модели предполагается, что можно найти уравнение, удовлетворительно описывающее значение тренда. В обоих изложенных выше примерах эти предпосылка была успешно выполнена. Тренда, который нами рассматривался, был очевидно линейный. Если бы исследуемый тренд представлял собой кривую, мы были бы вынуждены моделировать эту связь с помощью одного из методов формализации нелинейных взаимосвязей, рассмотренных в предыдущей главе. После того, как параметры уравнения тренда определены, процедура составления прогнозов становится совершенно очевидной. Прогнозные значения определяются по формуле:
F= Т  S,
S,
где
Т=64,6+1,36  номер квартала (тыс. шт. за квартал),
номер квартала (тыс. шт. за квартал),
а сезонные компоненты составляют 1,116 в первом квартале, 1,097 - во втором, 0,922 - в третьем и 1,055 в четвертом квартале. Ближайший следующий квартал - это второй квартал 1999., охватывающий период с апреля по июнь и имеющий во временном ряду порядковый номер 14. Прогноз объема продаж в этом квартале составляет:
F= Т  S = (64 + 1,36
S = (64 + 1,36  14)
14)  0,907 = 83,64
0,907 = 83,64  0,907 = 75,9 (тыс. шт. за квартал).
0,907 = 75,9 (тыс. шт. за квартал).
С учетом величины ошибки прогноза мы можем сделать вывод, что данная оценка будет отклоняться от фактического значения не более, чем на 2 - 3 %. Аналогично, прогноз на октябрь-декабрь 1999 г., рассчитывается для квартала с порядковым номером 16 с использованием значения сезонной компоненты для IV квартала года:
F = Т  S = (64 + 1,36
S = (64 + 1,36  16)
16)  1,055 = 83,36
1,055 = 83,36  1,055 = 91,1(тыс. шт. за квартал).
1,055 = 91,1(тыс. шт. за квартал).
Разумно предположить, что величина ошибки данного прогноза будет несколько выше, чем предыдущего, поскольку этот прогноз рассчитан на более длительную перспективу.
Резюме
Под временным рядом понимается любое множество данных, относящихся к определенным моментам времени. Это могут быть, скажем, годы, кварталы, месяцы или недели. В моделях временного ряда ретроспективная тенденция используется для прогнозирования поведения переменной в будущем. Краткосрочные прогнозы являются более точными, чем долгосрочные. Если прогноз составлялся на более длительный период времени при условии, что существующая тенденция сохранится в будущем, то тем больше величина ошибки.
Для моделирования временных рядов используются два типа моделей - аддитивная и мультипликативная. В обоих случаях предполагается, что значение переменной и включает в себя ряд компонент. Временной ряд может состоять из собственно тренда - общей тенденции изменения значений переменной; сезонной вариации - краткосрочных периодических колебаний значений переменной; циклической вариации - долгосрочных периодических колебаний значений переменной; ошибки или остатка. В данном учебном пособии не рассматривались массивы данных за длительные промежутки времени, содержащие циклическую вариацию.
Рассмотренные нами модели имеют следующий вид:
Аддитивная А = Т + S + Е
Мультипликативная А = Т  S
S  Е.
Е.
В обоих видах моделей для десезонализации данных применяется метод скользящего среднего. Затем десезонализированные данные используются при построении модели тренда. По этой модели составляют прогнозы будущих значений тренда. В случае линейной модели для нахождения параметров прямой, наилучшим образом аппроксимирующей фактические значения, используется метод наложения квадратов. Процесс построения нелинейных моделей гораздо более сложен.
В отличие от линейных регрессионных моделей для оценки обоснованности или точности прогнозных моделей статистические методы, как правило, не используются. Наилучшую среди нескольких моделей выбирает специалист, составляющий прогноз. Чтобы определить, насколько точно рассматриваемая модель аппроксимирует прошлые данные, применяются два показателя:
Среднее абсолютное отклонение (МАD)= 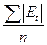 .
.
Среднеквадратическая ошибка (МSE)= 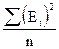 .
.
4.3. Автокорреляция и авторегрессия между уровнями временного ряда
Во многих временных рядах можно наблюдать зависимость t -го уровня yt от предшествующих yt-τ,. Это можно сказать, например, о динамике численности населения, занятых, промышленно-производственного персонала, цен и тарифов, урожайности сельскохозяйственных культур и т.д.
Зависимость между последовательными (соседними) уровнями временного ряда называется автокорреляцией.
Измерить автокорреляцию между уровнями ряда можно с помощью коэффициентов автокорреляции.
Коэффициенты автокорреляции можно рассчитывать между уровнями временного ряда, сдвинутыми на любое число промежутков времени τ. Этот сдвиг называется временным лагом. Он определяет порядок коэффициента автокорреляции. При τ = 1 речь идет о коэффициенте автокорреляции 1-го порядка, т.е. между соседними уровнями; при τ = 2 - о коэффициенте автокорреляции 2-го порядка, т.е. при сдвиге уровней на 2 периода, и т.д.
Коэффициент автокорреляции между уровнями временного ряда можно рассчитать с помощью различных формул. Приведем одну из них:
 (4.9),
(4.9),
где 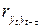 - коэффициент автокорреляции между уровнями исходного ряда yt и уровнями ряда, сдвинутыми по отношению к уровням исходного ряда на t лет yt - t.
- коэффициент автокорреляции между уровнями исходного ряда yt и уровнями ряда, сдвинутыми по отношению к уровням исходного ряда на t лет yt - t.
При этом временной лаг t часто называют тау-сдвигом.
Заметим, что расчет может быть осуществлен и по другим формулам.
Анализ матрицы коэффициентов автокорреляции различных порядков помогает при выявлении периодичности во временных рядах.
Рассчитаем коэффициент автокорреляции 1-го порядка для нашего примера.
Промежуточные расчеты проведем в рабочей таблице (4.7):
Таблица 4.7.
| yt | yt-1 | ytyt-1 | yt2 | (yt-1)2 | |
| 516,40 | 569,70 | 294193,08 | 266668,96 | 324558,09 | |
| 472,00 | 516,40 | 243740,80 | 222784,00 | 266668,96 | |
| 431,00 | 472,00 | 203432,00 | 185761,00 | 222784,00 | |
| 395,80 | 431,00 | 170589,80 | 156657,64 | 185761,00 | |
| 365,10 | 395,80 | 144506,58 | 133298,01 | 156657,64 | |
| Суммы | 2180,30 | 2384,90 | 1056462,26 | 965169,61 | 1156429,69 |
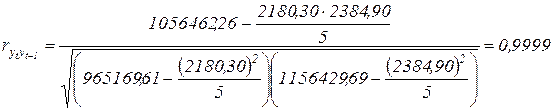 .
.
Близкое к единице значение коэффициента автокорреляции первого порядка свидетельствует о тесной прямой связи между текущими и непосредственно предшествующими уровнями временного ряда или, иными словами, о наличии во временном ряде тенденции.
Автокорреляция в остатках. Для анализа качества уравнения тренда можно рассчитать коэффициент автокорреляции по остаткам (отклонениям от тренда): 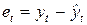 .
.
В этом случае формула расчета примет вид:
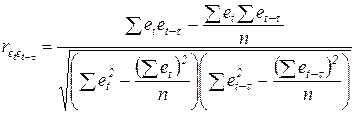 .
.
Чем ближе к нулю этот коэффициент, тем лучше подобрана функциональная форма модели тренда.
Рассчитаем коэффициент автокорреляции 1-го порядка для нашего примера.
Промежуточные расчеты проведем в рабочей таблице (4.8).
Таблица 4.8
| et | et-1 | etet-1 | et2 | (et-1)2 | |
| -3,04 | 9,52 | -28,94 | 9,24 | 90,70 | |
| -6,70 | -3,04 | 20,37 | 44,92 | 9,24 | |
| -6,96 | -6,70 | 46,68 | 48,51 | 44,92 | |
| -1,43 | -6,96 | 9,94 | 2,04 | 48,51 | |
| 8,61 | -1,43 | -12,29 | 74,12 | 2,04 | |
| Суммы | -9,52 | -8,61 | 35,75 | 178,82 | 195,40 |
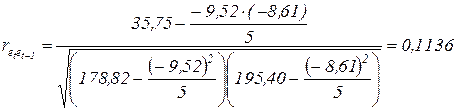 .
.
Близость коэффициента автокорреляции  к нулю свидетельствует об адекватности выбранной модели.
к нулю свидетельствует об адекватности выбранной модели.
Для характеристики автокорреляции используется критерий Дарбина-Уотсона, который исчисляется по формуле:
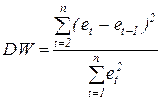 .
.
Если DW равен 2, то автокорреляция полностью отсутствует, если DW равен 0 или 4 имеет место полная автокорреляция.
Существуют таблицы значений этого критерия. Они составлены для различных уровней значимости α. Входами в них являются число наблюдений n и число объясняющих переменных в уравнении регрессии v.
В них приведены верхние DWU и нижние DWL критические границы критерия DW.
Для проверки нулевой гипотезы об отсутствии автокорреляции в остатках фактическое значение DW сравнивается с табличными DWU и DWL:
1) если DW > DWU (до 4 - DWU), гипотеза об отсутствии автокорреляции принимается;
2) если DW < DWL, гипотеза об отсутствии автокорреляции отвергается;
3) если DWL < DW < DWU или (4 - DWU) < DW < (4 - DWL), ничего определенного сказать нельзя и требуется дальнейшее исследование (например, уточнение уравнения тренда, увеличение числа наблюдений и пр.);
4) если DW > (4 — DWL), имеет место отрицательная автокорреляция.
Для иллюстрации расчета критерия Дарбина-Уотсона воспользуемся данными нашего примера.
Промежуточные расчеты приведем в таблице (4.9):
Таблица 4.9
| et | et-1 | (et)2 | Et-et-1 | (et-et-1)2 | |
| 9,52 | 90,70 | ||||
| -3,04 | 9,52 | 9,24 | -12,56 | 157,8254 | |
| -6,70 | -3,04 | 44,92 | -3,66 | 13,4165 | |
| -6,96 | -6,70 | 48,51 | -0,26 | 0,0691 | |
| -1,43 | -6,96 | 2,04 | 5,54 | 30,6600 | |
| 8,61 | -1,43 | 74,12 | 10,04 | 100,7442 | |
| Суммы | -9,52 | -8,61 | 269,52 | -0,91 | 302,72 |
 .
.
Таблица значений критерия Дарбина-Уотсона начинается с п = 15, но все, что относится к п = 15, может быть использовано и для п < 15.
Поскольку в нашем примере для выравнивания использовалась линейная функция с одной переменной t, то v= 1.
При α=0,05 для п= 15 верхняя граница DWU = 1,36, а нижняя DWL – 1,08.
Рассчитанное же нами фактическое значение DW = 1,21.
Так как DWL < DW < DWU ничего определенного об автокорреляции остатков сказать на уровне значимости α = 0,05 нельзя и требуется дальнейшее исследование.
Таким образом, нам не удалось подтвердить адекватность линейного уравнения тренда.
Прогнозирование по уравнению авторегрессии. При наличии автокорреляции между уровнями временного ряда каждый его уровень уt можно рассматривать как функцию предыдущих уровней.
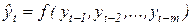 ,
,
где m - число уровней ряда, включенных в уравнение в качестве переменных и определяющих порядок авторегрессии.
Уравнение, выражающее эту зависимость, называется уравнением авторегрессии.
Наиболее простой формой зависимости между соседними уровнями ряда является линейное уравнение авторегрессии 1-го порядка:
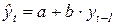 .
.
Параметры уравнения авторегрессии определяется по общим правилам регрессионного анализа.
Продолжим рассмотрение нашего примера:
| yt | yt-1 | ytyt-1 | yt2 | (yt-1)2 | |
| 516,40 | 569,70 | 294193,08 | 266668,96 | 324558,09 | |
| 472,00 | 516,40 | 243740,80 | 222784,00 | 266668,96 | |
| 431,00 | 472,00 | 203432,00 | 185761,00 | 222784,00 | |
| 395,80 | 431,00 | 170589,80 | 156657,64 | 185761,00 | |
| 365,10 | 395,80 | 144506,58 | 133298,01 | 156657,64 | |
| Суммы | 2180,30 | 2384,90 | 1056462,26 | 965169,61 | 1156429,69 |
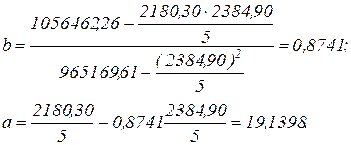
Таким образом, авторегрессионная модель будет иметь вид:
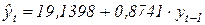 .
.
Это уравнение можно использовать как для выравнивания временного ряда, так и для прогнозирования.
Приведем фактические и выравненные по уравнению авторегрессии уровни временного ряда:
| yt | 
| |
| 516,40 | 517,10 | |
| 472,00 | 470,52 | |
| 431,00 | 431,71 | |
| 395,80 | 395,87 | |
| 365,10 | 365,10 |
Стандартная ошибка уравнения регрессии Syx = 1,03328, наблюдаемое значение F – критерия = 13510,56. Очевидно, что данное уравнение хорошо отражает характер зависимости между последовательными уровнями ряда.
Сделаем прогноз среднегодовой численности ППП в Ростовской области на 1999 год.
Подставляя в найденное уравнение среднегодовую численность ППП в 1998 году, получим 338,27 тыс.чел.:
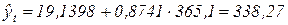 .
.
Дата публикования: 2015-10-09; Прочитано: 1244 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
