 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры решения типовых задач
|
|
Пример 1. Доказать непрерывность функции 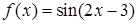 при любом значении
при любом значении 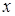 , пользуясь определением непрерывности функции
, пользуясь определением непрерывности функции  .
.
Решение. Возьмем любое значение  на числовой оси и составим разность:
на числовой оси и составим разность: 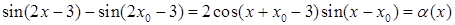 .
.
Так как 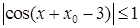 , а
, а 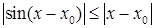 , то при
, то при 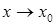
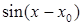 есть бесконечно малая функция. Следовательно, и
есть бесконечно малая функция. Следовательно, и  бесконечно мала при
бесконечно мала при 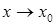 как произведение ограниченной функции на бесконечно малую функцию. Отсюда следует, что
как произведение ограниченной функции на бесконечно малую функцию. Отсюда следует, что  . Непрерывность
. Непрерывность  , таким образом, показана.
, таким образом, показана.
Пример 2. Дана функция 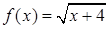 . Доказать на «
. Доказать на « »-языке непрерывность функции в точке
»-языке непрерывность функции в точке 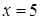 .
.
Решение. В точке 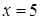 функция определена:
функция определена: 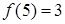 .
.
Зададим 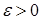 . Составим разность
. Составим разность 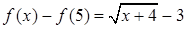 и оценим ее по модулю. При
и оценим ее по модулю. При 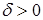 для значений
для значений 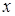 , удовлетворяющих неравенству
, удовлетворяющих неравенству 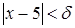 , будет также выполняться и неравенство
, будет также выполняться и неравенство
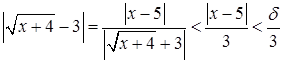 .
.
Если положить  , т. е.
, т. е. 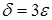 , то при значениях
, то при значениях 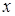 , для которых
, для которых 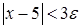 , будет выполняться неравенство
, будет выполняться неравенство 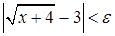 . Непрерывность функции при
. Непрерывность функции при 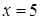 доказана.
доказана.
Пример 3. Дана функция 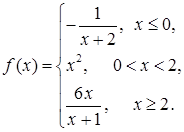 . Исследовать ее на непрерывность. Найти точки разрыва функции, если они существуют. Определить характер точек разрыва и величину скачка. Построить график
. Исследовать ее на непрерывность. Найти точки разрыва функции, если они существуют. Определить характер точек разрыва и величину скачка. Построить график 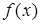 .
.
Решение. Функция 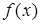 является неэлементарной, так как представлена различными аналитическими выражениями на промежутках
является неэлементарной, так как представлена различными аналитическими выражениями на промежутках 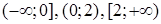 . Внутри первого промежутка элементарная функция
. Внутри первого промежутка элементарная функция 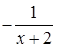 имеет разрыв при
имеет разрыв при  . Разрыв также возможен в точках перехода от одного аналитического выражения к другому, т.е. в точках
. Разрыв также возможен в точках перехода от одного аналитического выражения к другому, т.е. в точках 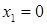 и
и 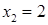 , и в точке
, и в точке  .
.
Исследуем непрерывность в точке 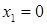 :
:
 т.е
т.е 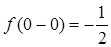 ;
;
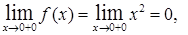 т.е
т.е 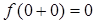 ;
;
Так как  , то функция
, то функция 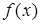 в точке
в точке 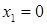 имеет разрыв первого рода. Найдем значение функции в точке
имеет разрыв первого рода. Найдем значение функции в точке 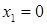 :
: 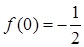 (т.к.
(т.к. 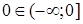 ). Так как
). Так как 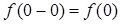 , то функция непрерывна в этой точке слева.
, то функция непрерывна в этой точке слева.
Для точки 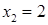 имеем:
имеем:
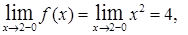 т.е
т.е 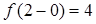 ;
;
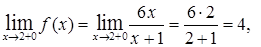 т.е
т.е 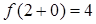 .
.
Так как  , то
, то 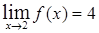 . Найдем значение функции в точке
. Найдем значение функции в точке 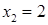 :
: 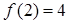 (т.к.
(т.к. 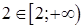 ). Таким образом
). Таким образом 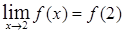 . Итак, функция непрерывна в точке
. Итак, функция непрерывна в точке 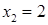 .
.
Наконец, для точки  находим:
находим:
 т.е
т.е 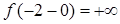 ;
;
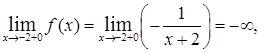 т.е
т.е 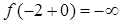 .
.
Таким образом, в точке  функция имеет разрыв второго рода (бесконечный скачок).
функция имеет разрыв второго рода (бесконечный скачок).
График функции представлен на рис. 4.

Пример 4. Исследовать функцию 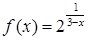 на непрерывность. Построить график
на непрерывность. Построить график 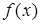 .
.
Решение. Так как 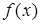 – элементарная функция, определенная для всех
– элементарная функция, определенная для всех 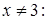
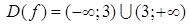 , поэтому она непрерывна на всей области определения.
, поэтому она непрерывна на всей области определения.
Поскольку значение 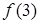 не определено, функция терпит разрыв в точке
не определено, функция терпит разрыв в точке 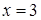 .
.
Найдем односторонние пределы в точке 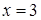

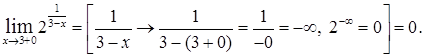
Так как 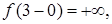 в точке
в точке 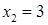 имеет место разрыв функции II рода.
имеет место разрыв функции II рода.
Для того, чтобы построить график 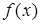 , вычислим пределы функции при
, вычислим пределы функции при 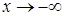 и
и 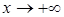 :
:
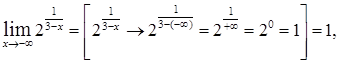
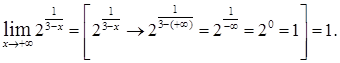
График функции 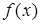 изображен на рис.5.
изображен на рис.5.

Пример 5. Найти точки разрыва функции 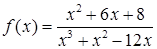 , установить их род. В точках устранимого разрыва доопределить функцию таким образом, чтобы она стала непрерывной.
, установить их род. В точках устранимого разрыва доопределить функцию таким образом, чтобы она стала непрерывной.
Решение. Так как 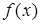 яляется элементарной функцией, определенной для всех
яляется элементарной функцией, определенной для всех 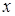 , для которых
, для которых 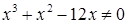 , т.е.
, т.е. 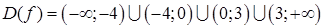 , то она непрерывна на всей области определения.
, то она непрерывна на всей области определения.
Поскольку значения 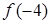 ,
, 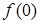 и
и 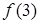 не определены, функция терпит разрыв в точках
не определены, функция терпит разрыв в точках 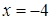 ,
, 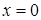 и
и 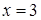 .
.
Найдем односторонние пределы в точке 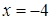 :
:
 , т.е
, т.е 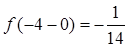 ;
;
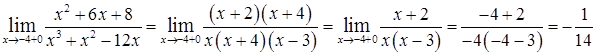 , т.е
, т.е 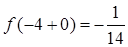 .
.
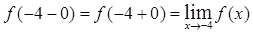 , но значение
, но значение 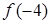 не определено. Таким образом, в точке
не определено. Таким образом, в точке 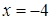 имеет место разрыв I рода (устранимый разрыв).
имеет место разрыв I рода (устранимый разрыв).
Доопределим функцию в точке 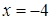 таким образом, чтобы она стала непрерывной в этой точке.
таким образом, чтобы она стала непрерывной в этой точке.
По определению непрерывности функции в точке должно иметь место равенство 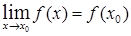 . т. е.
. т. е. 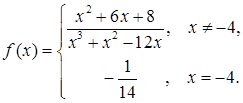
Найдем односторонние пределы в точке 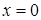 :
:
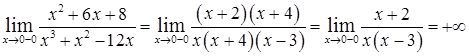 ,
,
т.е 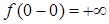
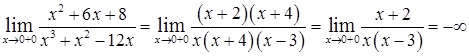 ,
,
т.е 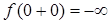 .
.
Таким образом, в точке 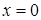 имеет место разрыв II рода (бесконечный скачок).
имеет место разрыв II рода (бесконечный скачок).
Найдем односторонние пределы в точке 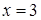 :
:
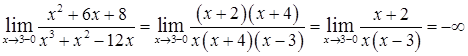 ,
,
т.е 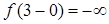
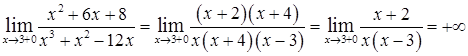 ,
,
т.е  .
.
Таким образом, в точке 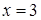 имеет место разрыв II рода (бесконечный скачок).
имеет место разрыв II рода (бесконечный скачок).
Пример 6. Исследовать на равномерную непрерывность функцию 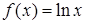 на промежутке
на промежутке 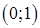 .
.
Решение. Эта функция не является равномерно непрерывной на промежутке 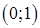 . Зададим
. Зададим 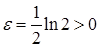 .
.
Возьмем 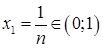 и
и 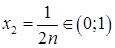 , где
, где 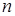 – натуральное число. Тогда
– натуральное число. Тогда  .
.
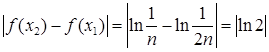 .
.
Какое бы 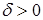 мы ни выбрали,
мы ни выбрали, 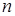 можно выбрать настолько большим, что будет
можно выбрать настолько большим, что будет  , при этом
, при этом 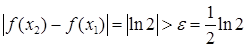 . Это противоречит определению равномерно непрерывной функции.
. Это противоречит определению равномерно непрерывной функции.
Пример 7. Показать, что функция 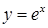 на промежутке
на промежутке 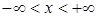 не является равномерно непрерывной.
не является равномерно непрерывной.
Решение. Зафиксируем 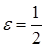 . Взяв
. Взяв 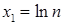 и
и  , получим
, получим  при
при 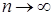 , значит,
, значит,  , но
, но 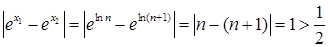 .
.
Задания для самостоятельной работы
n 39. Исходя из определения непрерывности функции в терминах « », доказать непрерывность функций:
», доказать непрерывность функций:
а) 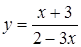 в точке в точке 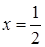 ; ;
| б) 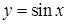 для для  ; ;
|
в) 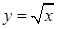 для для 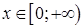 ; ;
| г) 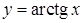 для для  ; ;
|
д) 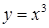 для для  ; ;
| е) 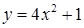 для для  ; ;
|
ж) 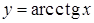 для для  ; ;
| з)  для для  ; ;
|
и)  для для  ; ;
| к) 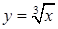 для для  . .
|
n 40. Исследовать данную функцию на непрерывность. Найти точки разрыва функции, если они существуют. Определить характер точек разрыва и величину скачка. Построить график функции.
а) 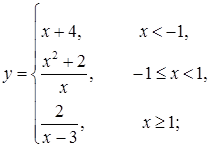
| б) 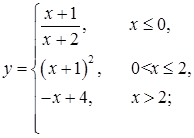
|
в) 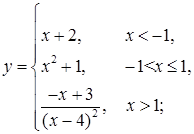
| г) 
|
д) 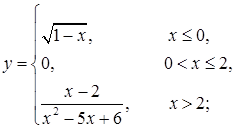
| е) 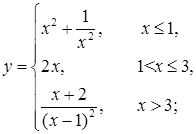
|
ж) 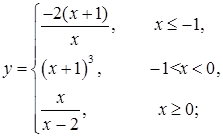
| з) 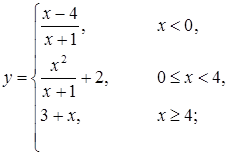
|
и) 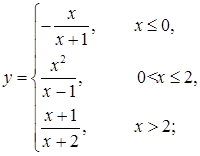
| к) 
|
n 41. Исследовать функцию на непрерывность. Построить график функции.
а) 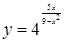 ; ;
| б) 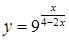 ; ;
|
в) 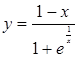 ; ;
| г) 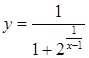 ; ;
|
д) 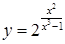 ; ;
| е) 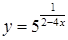 ; ;
|
ж) 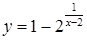 ; ;
| з) 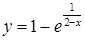 ; ;
|
и) 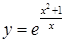 ; ;
| к) 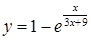 . .
|
n 42. Найти точки разрыва функции, установить их характер. В точках устранимого разрыва доопределить функцию таким образом, чтобы она стала непрерывной.
а) 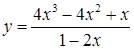 ; ;
| б) 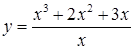 ; ;
|
в)  ; ;
| г)  ; ;
|
д) 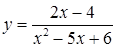 ; ;
| е) 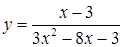 ; ;
|
ж) 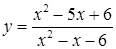 ; ;
| з) 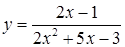 ; ;
|
и) 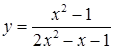 ; ;
| к) 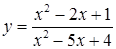 . .
|
n 43. Исследовать на равномерную непрерывность в заданных областях следующие функции:
Дата публикования: 2015-09-17; Прочитано: 7990 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
