 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тема 1. Системы счисления. Совокупность приемов и методов записи чисел называется системой счисления
|
|
Совокупность приемов и методов записи чисел называется системой счисления. Системы счисления бывают:
1. Непозиционные (значение символа не зависит от его положения в числе).
Пример 1. Система с одним символом (палочкой). Встречалось у многих народов. Число записывалось количеством палочек.
Пример 2. Римская с набором символов I(1), V(5), X(10), L(50), C(100), D(500), M(1000)… Есть отклонение от правила независимости положения цифры в числе (LХ и XL – 60 и 40).
2. Позиционные. Значение цифры определяется положением в числе.
Пример. 222 – 2 сотни, 2 десятка, 2 единицы.
Любая позиционная система счисления характеризуется основанием. Основание (базис) q позиционной системы счисления – количество знаков или символов, используемых для изображения в данной системе. В следующей таблице приведены характеристики основных систем счисления.
| Название системы счисления | Основание | Базисные числа |
| Двоичная | 0, 1 | |
| Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 | |
| Десятичная | 0 – 9 | |
| Шестнадцатеричная | 0 – 9, a, b, c, d, e, f |
Для позиционной системы счисления справедливо равенство:
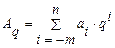
или
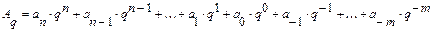 ,
,
где A q – десятичный эквивалент числа, записанного в системе счисления с основанием q; ai – i -ая цифра числа a; n +1, m – количество целых и дробных разрядов.
Пример (для десятичной системы счисления):
507,41=5*102+0*101+7*100+4*10-1+1*10-2.
¨ Перевод целых чисел из одной системы счисления в другую делением на основание новой системы счисления.
Исходное число делят на основание новой системы счисления, переведенное в систему счисления исходного числа. Затем неполное частное, полученное от такого деления, нужно снова разделить на основание новой системы счисления. Таким образом поступают до тех пор, пока неполное частное не станет равным нулю. Полученный результат представляет собой остатки от деления, записанные в порядке, обратном их получению.
¨ Перевод правильных дробей умножением на основание новой системы счисления.
Исходное число умножают на основание новой системы счисления, переведенное в систему счисления исходного числа. Затем дробную часть от полученного произведения снова умножают на основание новой системы счисления. При переводе правильных дробей можно получить дробь в виде бесконечного расходящегося ряда. Процесс перевода заканчивается, если появится дробная часть, имеющая во всех разрядах нули, или если будет достигнута требуемая точность (получено требуемое количество разрядов результата).
¨ Перевод смешанных чисел.
Для перевода неправильных дробей необходим раздельный перевод целой и дробной частей по правилам, описанным выше.
¨ Перевод из восьмеричной в двоичную систему счисления триадами.
Исходное число разбивается на триады справа налево для целых чисел и слева направо для правильной дроби, затем заменяем каждую триаду двоичным эквивалентом. Двоичные эквиваленты восьмеричных цифр представлены в следующей таблице.
| восьмеричная цифра | ||||||||
| двоичный эквивалент |
¨ Перевод из двоичной в восьмеричную и шестнадцатеричную систему счисления.
Триады (тетрады) исходного числа справа налево для целых чисел и слева направо для правильной дроби заменяются соответствующей восьмеричной цифрой.
¨ Сложение и умножение в системах счисления с основанием 2, 8, 16.
Существуют таблицы сложения и умножения для указанных систем счисления.
Сложение и умножение выполняются аналогично десятичной системе счисления. При этом удобно пользоваться представленными ниже таблицами.
Сложение в двоичной системе счисления
| + | ||
Сложение в восьмеричной системе счисления
| + | ||||||||
Сложение в шестнадцатеричной системе счисления
| + | А | В | С | D | Е | F | ||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| А | В | С | D | Е | F | |||||||||||
| A | A | В | С | D | Е | F | ||||||||||
| B | B | С | D | Е | F | 1A | ||||||||||
| C | C | D | Е | F | 1A | 1B | ||||||||||
| D | D | Е | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1Е |
Умножение в двоичной системе счисления
| * | ||
Умножение в восьмеричной системе счисления
| + | ||||||||
Умножение в шестнадцатеричной системе счисления
| + | А | В | С | D | Е | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | C | E | 1A | 1C | 1E | |||||||||||
| C | F | 1B | 1E | 2A | 2D | |||||||||||
| C | 1C | 2C | 3C | |||||||||||||
| A | F | 1E | 2D | 3C | 4B | |||||||||||
| C | 1E | 2A | 3C | 4E | 5A | |||||||||||
| E | 1C | 2A | 3F | 4D | 5B | |||||||||||
| 1B | 2D | 3F | 5A | 6C | 7E | |||||||||||
| A | A | 1E | 3C | 5A | 6E | 8C | ||||||||||
| B | B | 2C | 4D | 6E | 8F | 9A | A5 | |||||||||
| C | C | 3C | 6C | 9C | A8 | B4 | ||||||||||
| D | D | 1A | 4E | 5B | 8F | 9C | A9 | B6 | C3 | |||||||
| E | E | 1C | 2A | 7E | 8C | 9A | A8 | B6 | C4 | D2 | ||||||
| F | F | 1E | 2D | 3C | 4B | 5A | A5 | B4 | C3 | D2 | E1 |
¨ Двоично-десятичная система счисления
Двоично-десятичная система счисления широко используется в цифровых устройствах, когда основная часть операций связана не с обработкой и хранением вводимой информации, а с ее вводом и выводом на какие-либо индикаторы с десятичным представлением полученных результатов (микрокалькуляторы, кассовые аппараты и т. п.).
В двоично-десятичной системе десятичные цифры от 0 до 9 представляют 4-разрядными двоичными комбинациями от 0000 до 1001, т. е. двоичными эквивалентами десяти первых шестнадцатеричных цифр. Преобразования из двоично-десятичной системы в десятичную (и обратные преобразования) не вызывают затруднений и выполняются путем прямой замены четырех двоичных цифр одной десятичной цифрой (или обратной замены).
Две двоично-десятичные цифры составляют 1 байт. Таким образом, с помощью 1 байта можно представлять значения от 0 до 99, а не от 0 до 255, как при использовании 8-разрядного двоичного числа. Используя 1 байт для представления каждых двух десятичных цифр, можно формировать двоично-десятичные числа с любым требуемым числом десятичных разрядов:
(1001 0101 0011 1000)2 = (38200)10;
(1001 0101 0011 1000)2-10=(9538)10.
Сложение двоично-десятичных чисел, имеющих один десятичный разряд, выполняется так же, как и сложение 4-разрядных двоичных чисел без знака, за исключением того, что при получении результата, превышающего 1001, необходимо производить коррекцию. Результат корректируется путем прибавления двоичного кода числа 6, т. е. кода 0110.
Если первоначальное двоичное сложение или прибавление корректирующего числа приводит к возникновению переноса, то при сложении многоразрядных двоично-десятичных чисел перенос осуществляется в следующий десятичный разряд.
Дата публикования: 2015-09-17; Прочитано: 433 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
