Эмпирическая функция распределения

По определению, эмпирическая функция распределения - это естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке. По оси абсцисс откладываются интервалы группирования данных, а по оси ординат – накопленная частость.

График эмпирической функции распределения по накопленным частотам представлен на рисунке 6:

Рисунок 6 – График эмпирической функции распределения

План эксперимента по выяснению регрессионной зависимости

1. Целью данного задания является установление регрессионной зависимости между тремя факторами (температура - X₁, давление - X₂, влажность - X₃) и откликом компьютерного эксперимента. Следовательно, количество возможных комбинаций 2³ = 8. Так как в нашем эксперименте значения отклика мы получаем с помощью компьютера, то количество повторов можно выбрать произвольно на заданных уровнях факторов, я считаю, что достаточно 5 повторов. В результате проведения эксперимента были получены значения отклика Y (таблица 8). С помощью ПФЭ найдем математическое описание процесса в окрестности точки факторного пространства с координатами: X₀₁ = 20°C, X₀₂ = 1 атм, X₀₃ = 0,55 и шагами варьирования: ΔX₁ = 20°C, ΔX₂ = 0,5 атм, ΔX₃ = 0,45.

Х_1min=0 °С, Х_1max=40 °С

Х_2min=0,5 атм._, Х_2max=1,5 атм.

Х_3min=0,1, Х_3max=1,0

2. Рассчитаем средние значения отклика, которые будут использоваться в качестве результата эксперимента по формулам (12), (13), результаты занесем таблицу 8.

Таблица 8 – Результаты компьютерного эксперимента и расчетов

№
Y1	241,027	10,1927	144,381	11,9076	232,399	0,0418024	129,766	2,34972
Y2	243,087	8,51102	142,766	13,8678	236,413	0,919956	128,315	2,487
Y3	239,495	11,7412	139,398	12,6462	233,021	1,51475	129,055	1,57699
Y4	240,38	10,4207	142,178	13,2803	232,694	4,67587	127,087	0,647587
Y5	240,692	14,485	135,943	7,71659	234,224	5,00082	127,914	0,846054
Yср	240,9362	11,07012	140,9332	11,8837	233,7502	2,43064	128,4274	1,58147
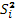
	1,770059	4,96309	11,0137	5,95848	2,6970057	5,11861	1,0646543	0,705797

Формулы для расчетов:

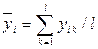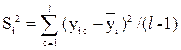, , (12), (13)

где l - число параллельных опытов в i -той строке матрицы: k - номер параллельного опыта.

3. Будем использовать полную линейную модель регрессии со взаимодействием (14). В том случае, если наша модель окажется проще, незначимые коэффициенты обратятся в 0, и мы их отбросим, так как будем проводить эксперимент на обезразмеренных величинах.

(14)

где θ_i – параметры модели;

X_i – факторы (независимые переменные);

Y_i – отклик.

4. Для упрощения обработки результатов эксперимента, производим кодирование значений факторов по выра­жению (15):

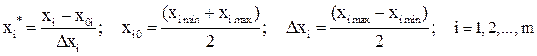, (15)

где - натуральное значение i-гофактора,

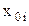- натуральное значение основного уровня (центра плана по фактору ),

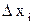- интервал варьирования фактора,

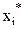- кодированный безразмерный фактор, который принимает значения .

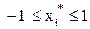То есть кодированные значения факторов равны: X^*₁=1- max, X^*₁= -1 – min; X^*₂= 1 – max, X^*₂= -1- min; X^*₃= 1 - max, X^*₃= -1 - min.

Таким образом, значения факторов:

Х_1min=0 °С, Х_1max=40 °С

Х_2min=0,5 атм._, Х_2max=1,5 атм.

Х_3min=0,1, Х_3max=1,0

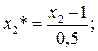
В результате такого кодирования получаем расширенную матрицу планирования полного факторного эксперимента в безраз­мерных величинах 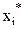. Далее мы будем иметь дело с кодированными переменными, поэтому звездочку будем опускать.

Строим расширенную матрицу планирования:

№ опыта	f0	f1=х1	f2=х2	f3=х3	f4=х1·х2	f5=х1·х3	f6=х2·х3	f7=х1·х2·х3
	+	+	+	+	+	+	+	+	240,9362
	+	-	+	+	-	-	+	-	11,07012
	+	+	-	+	-	+	-	-	140,9332
	+	-	-	+	+	-	-	+	11,8837
	+	+	+	-	+	-	-	-	233,7502
	+	-	+	-	-	+	-	+	2,43064
	+	+	-	-	-	-	+	+	128,4274
	+	-	-	-	+	+	+	-	1,58147
	ϴ0	ϴ1	ϴ2	ϴ3	ϴ4	ϴ5	ϴ6	ϴ7

5. Построенная матрица планирования является ортогональной, так как выполняются следующие соотношения 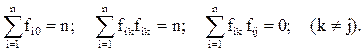(16):

(16)

6. Определим коэффициенты уравнения регрессии по выражению (17):

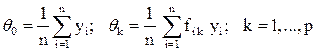. (17)

Согласно расширенной матрице плана, получим формулы для определения оценки для коэффициентов регрессии:

ϴ₀ = · (у₁+у₂+у₃+у₄+у₅+у₆+у₇+у₈),

ϴ₁ = · (у₁-у₂+у₃-у₄+у₅-у₆+у₇-у₈),

ϴ₂ = · (у₁+у₂-у₃-у₄+у₅+у₆-у₇-у₈),

ϴ₃ = · (у₁+у₂+у₃+у₄-у₅-у₆-у₇-у₈),

ϴ₄ = · (у₁-у₂-у₃+у₄+у₅-у₆-у₇+у₈),

ϴ₅ = · (у₁-у₂+у₃-у₄-у₅+у₆-у₇+у₈),

ϴ₆ = · (у₁+у₂-у₃-у₄-у₅-у₆+у₇+у₈),

ϴ₇ = · (у₁-у₂-у₃+у₄-у₅+у₆+у₇-у₈).

7. Произведем контроль воспроизводимости результатов исследова­ния, т.е. проверим равноточность измерений. Такая проверка необходима при малом числе опытов, т.к. в этом случае даже одна грубая ошибка может сильно исказить результаты. Проверка воспроизводимости производится с помощью критерия Кохрена, согласно которому, если имеются дисперсии по строкам и имеется их сумма 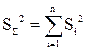, то для проверки равноточности необходимо выбрать самую большую из построчных дисперсий 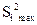и определить G – критерий

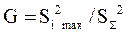, G = = 0,330827.

Сформулируем и проверим гипотезу об однородности дисперсий.

Н­₀: G < G_крит, дисперсии однородные,

Н₁: G > G_крит, дисперсии неоднородные.

По таблице значений критерия Кохрена для уровня значимости 0,05 найдем G_кр для числа степеней свободы 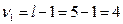и числа выборки 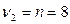, G_кр = 0,391.

Так как G=0,330827 < G_крит=0,391, можно сделать вывод, что опыты равноточные и дисперсии однородные, гипотеза Н₀ принимается.

8. Определим оценки коэффициентов регрессии по формулам, полученным в п.6:

ϴ₀ = · (240,9362+11,07012+140,9332+11,8837+233,7502+2,43064+ +128,4274 +1,58147) = 96,3766,

ϴ₁ = · (240,9362-11,07012+140,9332-11,8837+233,7502-2,43064+ +128,4274-1,58147) = 89,635,

ϴ₂ = · (240,9362+11,07012-140,9332-11,8837+233,7502+2,43064- -128,4274-1,58147) = 25,6702,

ϴ₃ = · (240,9362+11,07012+140,9332+11,8837-233,7502-2,43064- -128,4274-1,58147) = 4,82919,

ϴ₄ = · (240,9362-11,07012-140,9332+11,8837+233,7502-2,43064- -128,4274+1,58147) = 25,6613,

ϴ₅ = · (240,9362-11,07012+140,9332-11,8837-233,7502+2,43064- -128,4274+1,58147) = 0,09376,

ϴ₆ = · (240,9362+11,07012-140,9332-11,8837-233,7502-2,43064+ +128,4274+1,58147) = -0,872819,

ϴ₇ = · (240,9362-11,07012-140,9332+11,8837-233,7502+2,43064+ +128,4274-1,58147) = -0,45713.

9. Произведем оценку дисперсии воспроизводимости по формуле 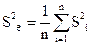(18): (18)

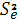= 4,1614245.

Определим дисперсию воспроизводимости для среднего значения отклика по формуле 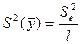: S² (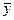) = 0,8322849.

Определим среднеквадратичное отклонение 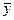по формуле 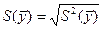S (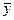) = 0,912296.

10. Произведем оценку значимости коэффициентов.

Сформулируем гипотезу:

Н₀: ϴ_i = 0 - коэффициент ϴ_i незначим;

Н₁: ϴ_i ≠ 0 - коэффициент ϴ_i значим.

Для проверки используется критерий Стьюдента t при уровне значимости 1-α/2 (α выбирается равным 0,05) и числе степеней свободы ν = = n(l -1) = 8·(5-1) = 32.

Для ортогонального планирования, оценки дисперсии коэффициентов уравнения регрессии равны между собой и определяются по формуле (19):

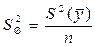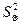, = 0,104036 (19)

Коэффициент уравнения статистически значим, если , где 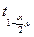значение критерия Стьюдента для уровня значимости α и числа степеней свободы ν:

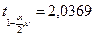при α = 0,975 и ν = 32.

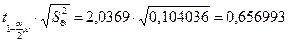
, 96,3766 > 0,656993, коэффициент уравнения статически значим, принимаем гипотезу Н₁.

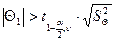, 89,635 > 0,656993, коэффициент уравнения статически значим, принимаем гипотезу Н₁.

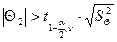, 25,6702 > 0,656993, коэффициент уравнения статически значим, принимаем гипотезу Н₁.

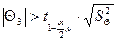, 4,82919 > 0,656993, коэффициент уравнения статически значим, принимаем гипотезу Н₁.

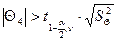, 25,6613 > 0,656993, коэффициент уравнения статически значим, принимаем гипотезу Н₁.

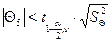, 0,09376 < 0,656993, коэффициент уравнения статически незначим, принимаем гипотезу Н₀.

, 0,872819 > 0,656993, коэффициент уравнения статически значим, принимаем гипотезу Н₁.

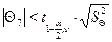, 0,45713 < 0,656993, коэффициент уравнения статически незначим, принимаем гипотезу Н₀.

Коэффициенты, признанные незначимыми (Θ₅ и Θ₇), приравняем к 0. Так как при ортогональном планировании коэффициенты уравнения регрессии оцениваются независимо друг от друга, то мы можем не производить пересчет коэффициентов и не проверять их значимость заново, а просто откинуть незначимые коэффициенты.

Статистическая незначимость некоторых коэффициентов может быть вызвана следующими причинами:

1. Большая ошибка эксперимента из-за наличия неуправляемых и неконтролируемых переменных.

2. Данный фактор или взаимодействие факторов действительно не ока­зывают существенного влияния на значение параметра отклика у.

Отбросив (приравняв к нулю) незначимые коэффициенты, получим уравнение связи между откликом у и факторами х_i:

y = f(x₁, x₂, x₃) = ϴ₀ + ϴ₁·x₁ + ϴ₂·x₂ + ϴ₃·x₃ + ϴ₄·x₁·x₂ + ϴ₆·x₂·x₃ + ε.

11. Оценим адекватность математической модели.

Для проверки адекватности полученной математической модели произ­водится оценка дисперсии адекватности:

,

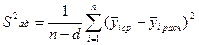где d = 6 - число значимых коэффициентов в уравнении; n = 8 - число опытов.

Найдем 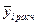, используя выбранную математическую модель и полученные коэффициенты регрессии.

= ϴ₀ + ϴ₁ + ϴ₂ + ϴ₃ + ϴ₄ + ϴ₆ = 241,29947_.

= ϴ₀ - ϴ₁ + ϴ₂ + ϴ₃ - ϴ₄ + ϴ₆ = 10,70687_.

= ϴ₀ + ϴ₁ - ϴ₂ + ϴ₃ - ϴ₄ - ϴ₆ = 140,3821_.

= ϴ₀ - ϴ₁ - ϴ₂ + ϴ₃ + ϴ₄ - ϴ₆ = 12,4347_.

= ϴ₀ + ϴ₁ + ϴ₂ - ϴ₃ + ϴ₄ - ϴ₆ = 233,3867_.

= ϴ₀ - ϴ₁ + ϴ₂ - ϴ₃ - ϴ₄ - ϴ₆ = 2,79413_.

= ϴ₀ + ϴ₁ - ϴ₂ - ϴ₃ - ϴ₄ + ϴ₆ = 128,9781_.

= ϴ₀ - ϴ₁ - ϴ₂ - ϴ₃ + ϴ₄ + ϴ₆ = 1,03069_.

Тогда S²_ад = 0,871040685.

Сформулируем гипотезу об адекватности модели:

Н­₀: F_крит> F – модель адекватна,

Н­₁: F_крит< F – модель не адекватна.

Для проверки гипотезы об адекватности воспользуемся критерием Фишера для выбранного уровня значимости α=0,05 и числа степеней свободы числителя при d = 6 и n = 8, 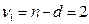, для знаменателя при 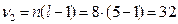. Найдем критическое значение критерия Фишера по таблице:

F_крит (0,05; 2; 32) = 3,295.

Вычислим расчетное значение критерия Фишера по формуле:

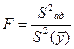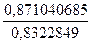= = 1,04657.

Сравнив рассчитанное и критическое значения критерия Фишера, получим F_крит > F, следовательно, данная модель является адекватной, принимаем гипотезу Н₀.

12. Запишем модель в размерном виде для всех значимых коэффициентов. Для того чтобы перевести модель в размерный вид необходимо перейти от безразмерных величин к размерным величинам для этого формулу 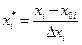подставляем в уравнение 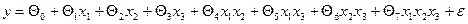, занулив при этом незначимые коэффициенты. В результате получаем:

y= .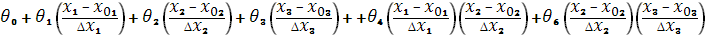

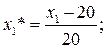
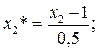
Рассчитаем новые коэффициенты:

Θ_0Р= -1,3119 ≈ -1,31;

Θ_1Р= 1,9156 ≈ 1,92;

Θ_2Р= 2,1512 ≈ 2,15;

Θ_3Р= 14,6108 ≈ 14,61;

Θ_4Р= 2,56613 ≈ 2,57;

Θ_6Р= -3,8793 ≈ -3,88.

Запишем математическую модель в окончательном виде:

y = -1,31 + 1,92·x₁ + 2,15·x₂ + 14,61·x₃ + 2,57·x₁·x₂ - 3,88·x₂·x₃.

13. Анализ робастности регрессионной модели.

Под анализом робастности понимается выяснение практической возможности полученной регрессионной модели.

Определяем коэффициент детерминации, который показывает долю общего рассеяния относительно среднего, обусловленного регрессионной зависимостью 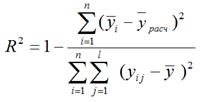(20):

(20)

где 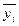- среднее по опыту;

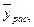- расчетные значения отклика;

- значение отклика для i-того опыта в j-том повторе;

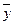- среднее средних значений по опыту;

i – количество опытов при каждом уровне фактора;

j – количество повторов в каждом опыте.

R² = 0,999995357.

Модель считается работоспособной, если R² > 0,75.

Таким образом, полученную регрессионную модель

y = -1,31 + 1,92·x₁ + 2,15·x₂ + 14,61·x₃ + 2,57·x₁·x₂ - 3,88·x₂·x₃ можно считать работоспособной, так как R² =0,999995357> 0,75.

Заключение

В результате проделанной работы мы познакомились с основными математическими статистическими методами планирования эксперимента, а также с методами анализа законов распределения вероятностей случайных величин. На первоначальном этапе была собрана априорная информация, необходимая для дальнейшего исследования, было выдвинуто предположение о виде закона распределения случайной величины и проведено доказательство данного предположения, были определены оценки параметров данного распределения. Во второй части работы выяснялась зависимость между факторами, действующими на исследуемую величину, и изменение этой величины. Для предвидения влияния определенных факторов используется полный факторный эксперимент для построения регрессионной математической модели. Эта модель позволяет нормировать измерения вне зависимости от влияющих факторов или указывает на влияющее воздействие, которое необходимо устранить.

Несмотря на простоту методов, они представляют собой мощный механизм повышения качества продукции и могут использоваться для решения весьма обширного круга задач, когда приходится принимать решения в условиях действия многочисленных влияющих на процесс факторов.

Преимущество простых статистических методов здесь выражается в том, что появляется возможность проведения корректировки производственного процесса еще тогда, когда в нем возникают некоторые отклонения, которые еще не приводят к браку, но уже создают угрозу появления дефектной продукции. Такое управление качеством процессов, называемое управлением по отклонениям, неизмеримо эффективнее, чем применяемый в настоящее время контроль качества продукции по результатам, при котором контролируется не процесс, а продукция на разных стадиях ее изготовления путем применения либо сплошного, либо выборочного статистического контроля.

Список использованной литературы

1. Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников. - М.: ФИЗМАТЛИТ, 2006. - 816 с. - ISBN 5-9221-0707-0.

2. ГОСТ Р ИСО 5479-2002 «Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения».

3. ГОСТ Р 50779.21–2004 (ИСО 2854:1976) «Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным».

4. Козлов М. В., Прохоров А. В. Введение в математическую статистику. – М.: Изд-во МГУ, 1987. - 264 с.