Пример 3. Расчет клиновидного бруса

На брус линейно переменной ширины действует равномерно

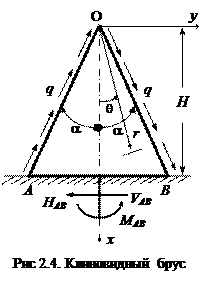распределенная вдоль граней касательная нагрузка (рис. 2.4). Объемные силы отсутствуют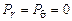

Напряжения определяются в полярной системе координат по формулам:

; ;

;

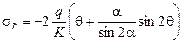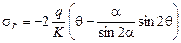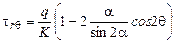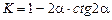. (2.3.1)

H = 4 м; a = =30°; q = 2 кН/м.

Требуется проверить, отвечает ли данное решение уравнениям плоской задачи теории упругости в полярной системе координат и граничным условиям конструкции. Кроме проверки граничных условий на гранях бруса, провести проверку также выполнение условий равновесия части отсеченного бруса радиуса r.

Построить эпюры напряжений в полярной системе координат в сечении радиуса r и горизонтальном сечении в прямоугольной системе координат, сравнив с решением сопротивления материалов аналогичной задачи.

1. Проверяем выполнение уравнений равновесия

; ;

;

.

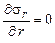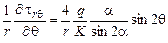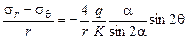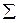
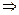
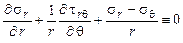б) ;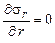

;

.

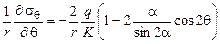
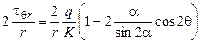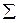
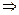
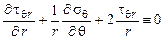Уравнения равновесия удовлетворяются.

2. Проверяем выполнение уравнения неразрывности деформаций

;

-

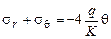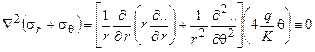Уравнение неразрывности деформаций удовлетворяется.

2. Проверяем выполнение граничных условий на гранях бруса.

Грань ОА . , ;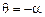

; ;

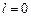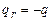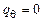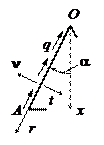a) .

;

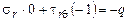
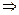
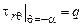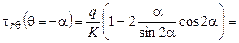
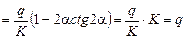б) ;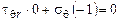

.

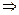
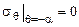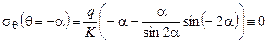Граничные условия на грани ОА выполнены.

Грань ОВ . , ;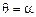

; ;

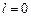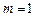a) .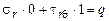

;

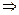
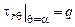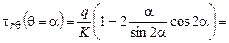
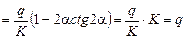б) ;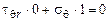

.

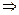
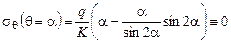Граничные условия на грани ОА выполнены.

Проверяем равновесие отсеченной части бруса (рис. 2.5).

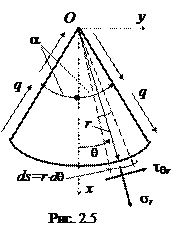1. ;

;

.

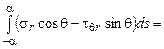
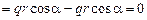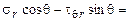
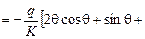
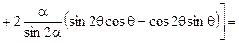
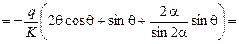
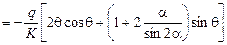Здесь и далее в преобразованиях используются формулы, приведенные в приложении I.

Так как подынтегральная функция обратно симметрична при интегрировании от -a до +a, то результат интегрирования равен нулю и первое условие равновесия выполняется.

2. ; ;

.

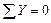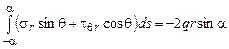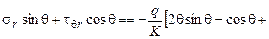
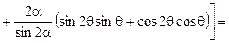
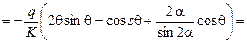
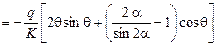Так как подынтегральная функция симметрична, то интервал интегрирования (-a, +a) можно заменить на интервал (0, +a), удвоив значение интеграла.

Интегрируя первое слагаемое по частям, получим

.

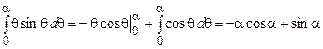Окончательно получаем

.

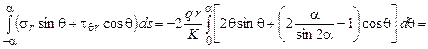
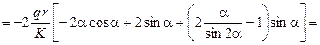
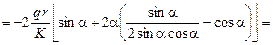
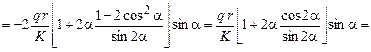
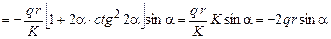Второе уравнение равновесия удовлетворяется.

3. ; 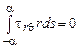или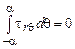

.

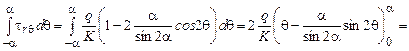
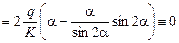Третье, моментное уравнение равновесия выполняется. Таким образом, часть клина, отсеченного сечением радиуса r, находится в равновесии под действием внешних и внутренних сил.

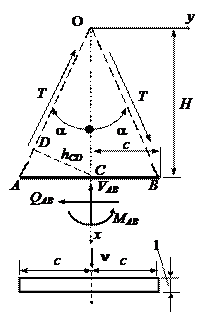Грань АВ x = H. l = 1; m = 0.

q_x ¹ 0; q_y ¹ 0;

; ;

;

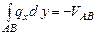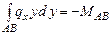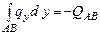Определяем опорные реакции:

; ;

.

; .

; .

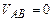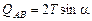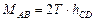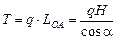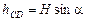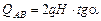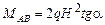Так как грань АВ не совпадает с полярной системой координат, то граничные условия формулируются в прямоугольно системе координат:

а. ;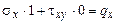

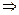
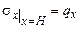б. .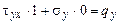

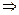
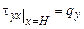Так как распределение нагрузок на грани АВ неизвестно, то интегрируя полученные условия получаем интегральные граничные условия:

а. ;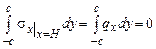

б.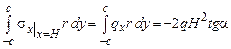

в. 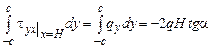. (2.3.2)

Чтобы проверить полученные условия, нужно выразить напряжения в прямоугольной системе координат через заданные напряжения в полярной системе координат. Для этого воспользуемся формулами напряжений на наклонных площадках [], (рис. 2.6, а):

;

;

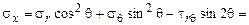
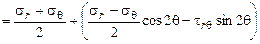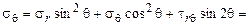
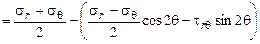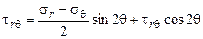; (2.3.3)

Подставляя формулы напряжений в полярной системе координат (2.3.1) в соотношения (2.3.2), получим:

; ;

;

; ;

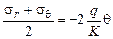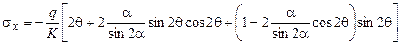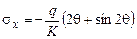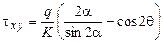. (2.3.4)

Заменяя в формулах интегральных граничных условий (2.3.2) напряжения в прямоугольной системе координат соотношениями (2.3.4) и заменяя интегрирование по у, на интегрирование по q (см. рис. 2. 6), проверяем выполнение интегральных граничных условий на грани АВ:

а. ,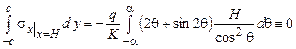

так как подынтегральная функция обратно симметрична.

б.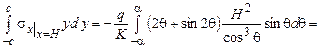

.

;

,

;

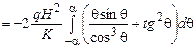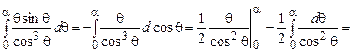
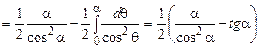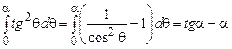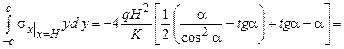
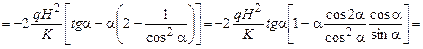
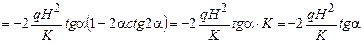в.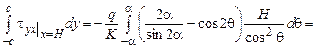

.

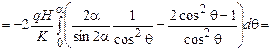
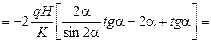
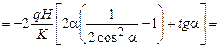
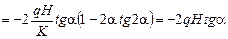Интегральные граничные условия на грани АВ удовлетворяются.

Так как удовлетворяются уравнения равновесия и все граничные условия, то формулы (2.3.1) являются решением задачи о равновесии клиновидного бруса.