Введение. Общая задача теории упругости описывается сложной системой 15 дифференциальных и алгебраических уравнений

Общая задача теории упругости описывается сложной системой 15 дифференциальных и алгебраических уравнений, решение которых представляет значительные трудности. Поэтому стремятся выделить классы задач, в которых можно ввести гипотезы, позволяющие снизить количество и порядок системы уравнений и тем упростить решение задачи. К одному из таких классов задач относится плоская задача теории упругости. включающая два типа задач плоское напряженное состояние и плоская деформация [1, 2, 3, 4].

При плоском напряженном состоянии рассматриваются тонкие пластинки постоянной толщины, на которую действует неизменная по толщине нагрузка, параллельная плоскости пластинки. Для плоского напряженного состояния принимают гипотезы об отсутствии нормальных напряжений и угловых деформаций перпендикулярных плоскости пластинки: 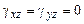(ось z перпендикулярна плоскости пластинки).

При плоской деформации рассматриваются длинные призматические тела, на которые действует в нормальной плоскости призматического тела неизменная по длине тела нагрузка. Принимается гипотеза об отсутствии перемещений вдоль оси тела 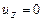и угловых параллельных оси призматического тела деформаций 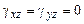(ось z, направлена вдоль оси призматического тела). Принятые гипотезы позволяют рассматривать плоскую пластинку малой постоянной толщины, в которой отсутствуют поперечные деформации . На основании закона Гука для плоской деформации определяем нормальные напряжения в сечениях, перпендикулярных оси тела, 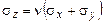( 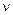- коэффициент Пуассона).

Для обоих типов плоской задачи теории упругости напряженно-деформированное состояние на зависит от координаты z и все функции, описывающие напряженно-деформированное состояние, являются функциями переменных х, у. В соответствии с принятыми гипотезами остаются 8 функций, определяющих напряженно-деформированное состояние плоской задачи теории упругости: 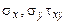- нормальные и касательные напряжения; 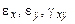- линейные и угловые деформации; 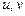- перемещения в плоскости пластинки. Соответственно, из системы уравнений общей задачи теории упругости остаются 8 уравнений: - 2 уравнения равновесия, 3 уравнения связи напряжений и деформаций – геометрические уравнения, 3 уравнения закона Гука. При решении задачи в напряжения используется 1 уравнение неразрывности деформаций.

Уравнения равновесия и геометрические уравнения для обоих типов задач совпадают. Физические уравнения закона Гука различны. Однако если ввести понятие приведенных модуля упругости Е ₁ и коэффициента Пуассона 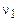, то закон Гука для обеих задач удается записать в общем виде.

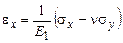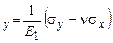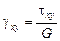, , . (1)

Приведенные модуль упругости и коэффициент Пуассона определяются формулами:

а) для плоского напряженного состояния , ;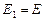

б) для плоской деформации , .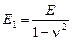

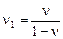Модуль сдвиг для обеих задач остается неизменным:

.

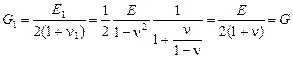В зависимости от формы пластинки (поперечного сечения призматического тела) задачу удобно решать в прямоугольной, полярной или другой специальной системе координат. Ниже рассматривается плоская задача теории упругости в прямоугольной и полярной системах координат.

При решении плоской задачи теории упругости толщину пластинки принимают условно равной единице (размерность принимается соответствующей размерностям, используемым для размеров пластинки в плане). При этом нагрузка рассчитывается равномерной распределенной по толщине пластинки равной единице.

Задача теории упругости может решаться в напряжениях, перемещениях или смешанным методом.

В работе рассматривается решение плоской задачи теории упругости в напряжениях. При решении задачи в напряжениях функции напряжений должны удовлетворять уравнениям равновесия, уравнению неразрывности деформаций и граничным условиям задачи.

В задании дается схема плоской задачи теории упругости и приводятся формулы нормальных и касательных напряжений. Необходимо проверить, являются ли приведенные формулы решением теории упругости для приведенной схемы:

1. Проверяется, удовлетворяют ли приведенные формулы напряжений уравнениям равновесия и уравнению неразрывности плоской задачи теории упругости – решение является решением плоской задачи теории упругости.

2. Формулируются граничные условия для каждой грани рассматриваемой схемы (конструкции).

3. Проверяется, удовлетворяют ли данные напряжения сформулированным граничным условиям – решение является решением рассматриваемой задачи.

Замечание. Если на некоторой грани АВ сформулированные граничные условия не выполняются или не могут быть сформулированы (например, в случае закрепления грани), то формулируются интегральные граничные условия:

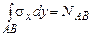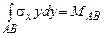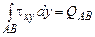, , , (1)

где 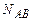, , 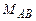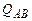- нормальная сила, изгибающий момент и поперечная сила на рассматриваемой грани, определяемые из условий равновесия конструкции в целом.

В случае выполнения интегральных граничных условий, считается на основе принципа Сен-Венана, что напряженное состояние, определяемое данными формулами напряжений, является решением данной задачи на расстоянии сравнимым размерами грани, где рассматриваются интегральные граничные условия. В самой зоне решение считается приближенным.

Для получения приведенных в задании решений, задаются некоторой функцией, в частности для прямоугольной области в прямоугольной системе координат полиномами переменных х, у с неизвестными коэффициентами. Далее, удовлетворяя уравнениям равновесия, уравнению неразрывности и граничным условиям, определяют неизвестные коэффициенты [6].

I. Плоская задача теории упругости