Теоретические сведения. Числовым рядом называется бесконечная последовательность чисел , соединенных знаком сложения:

Числовым рядом называется бесконечная последовательность чисел 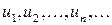, соединенных знаком сложения:

Числа 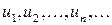называются членами ряда, а член - общим или n-м членом ряда.

Среди рядов особое место занимают степенные ряды, членами которых являются степенные функции аргумента х:

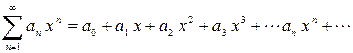
Действительные числа 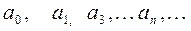называются коэффициентами ряда, х – действительная переменная.

Рассмотренный степенной ряд расположен по степеням х.

Имеют место ряды, расположенные по степеням 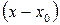, т.е. ряд вида

,

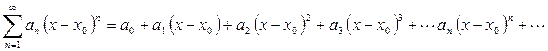где - некоторое постоянное число.

Для приложений важно уметь данную функцию f(x) разлагать в степенной ряд, т. е. функцию f(x) представлять в виде суммы степенного ряда.

Для любой функции f(x), определённой в окрестности точки и имеющей в ней производные до (n+1) -го порядка включительно, справедлива формула Тейлора:

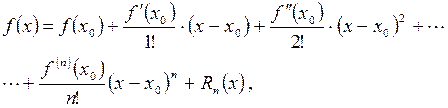
где , 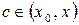- остаточный член в форме Лагранжа.

Число с можно записать в ви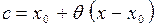де , где .

Без остаточного члена имеем – многочлен Тейлора:

.

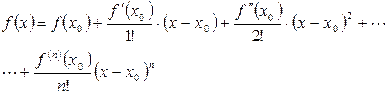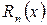Если функция f(x) имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки и остаточный член стремится к нулю при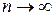 , то из формулы Тейлора получается разложение функции f(x) по степеням 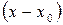, называемое рядом Тейлора:

.

Если в ряде Тейлора положить 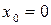, то получим разложение функции по степеням x в так называемый ряд Маклорена:

.

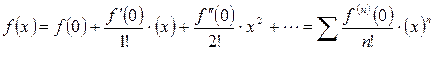Формально ряд Тейлора можно построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки . Но отсюда ещё не следует, что он будет сходиться к данной функции f(x); он может оказаться расходящимся или сходиться, но не к функции f(x).

Пример1. Разложить многочлен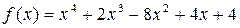

в ряд Тейлора при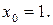

Решение:

Найдём производные данного многочлена:

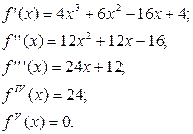
В точке 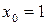имеем:

По формуле

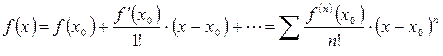
получаем:

Пример 2. Записать формулу Тейлора и выражение остаточного члена для

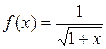
при n = 4 и

Решение:

Формула Тейлора имеет вид:

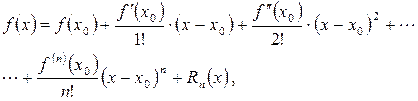
где

Найдём производные функции 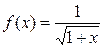в точке

Искомая формула имеет вид:

где и 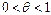, т.е.

.

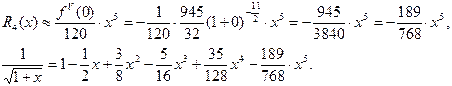Для того чтобы ряд Тейлора функции f(x)

сходился к f(x) в точке x, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора стремился к нулю при 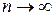, т. е. .

Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)

Для разложения функции f(x) в ряд Маклорена нужно:

1) Найти производные ;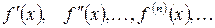

2) Вычислить значения производных в точке ;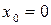

3) Написать ряд

для заданной функции и найти его интервал сходимости;

4) Найти интервал (-R; R), в котором остаточный член ряда Маклорена . Если такой интервал существует, то в нем функция f(x) и сумма ряда Маклорена совпадают.