Типові задачі. Задача 6.1. Розв’язати задачу Коші: , ,

Задача 6.1. Розв’язати задачу Коші: , , .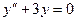

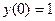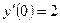
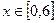Mathcad. 1)Розвязок задачі Коші за допомогою функції odesolve().

Given

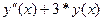= 0 символ похідної (‘) можна задати комбінацією клавіш Ctrl+F7 або за допомогою операції диференціювання на панелі інструментів «Аналіз»

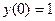
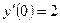початкові значення

y:= odesolve(x,6)

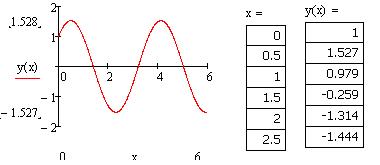
Результат розв’язку виводимо на графік. Також можна вивести таблицю значень:

2) Розвязок задачі Коші за допомогою функції rkfixed().

Для застосування функції rkfixed() рівняння або система рівнянь повинна бути представлена у нормальній формі Коші: 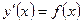. Так як у нас рівняння другого порядку, то його необхідно привести до системи рівнянь першого порядку:

,

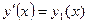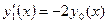
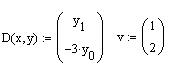Опишемо систему рівнянь вектором D(x,y) (перший параметр незалежна змінна) та задамо початкові наближення v:

Виведемо результати розв’язку на графіки:

, ,

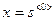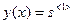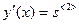
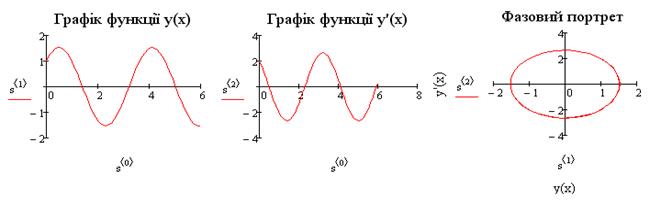
MATLAB. 1) Створимо М-файл для опису рівняння у нормальній формі Коші:

function out1 = vdp1(t,y)

out1 = [y(2); - 3*y(1)];

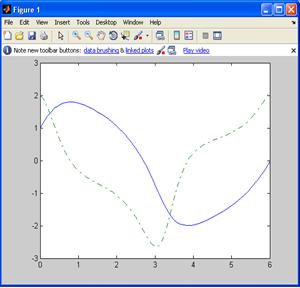
У командному вікні розв’яжемо рівняння за допомогою функції ode45() і побудуємо графік::

>> [t,y] = ode45('vdp1',[0 6],[1; 2]);

>> plot(t,y(:,1),'-',t,y(:,2),'-.')

де y(:,1) – перший стовпчик результуючої матриці що є значенням функції у(х);

y(:,2) – перший стовпчик – значення похідної.

2) Розв’яжемо систему диференціальних рівнянь, що описує електричний ланцюг з використанням блоку dee. , ,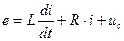

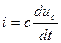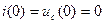
Представимо цю систему у нормальній формі Коші: ,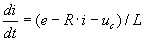

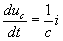
Що б скористатись блоком dee, необхідно шукані функції позначати х(і), а незалежні функції – u(i), то введемо позначення: , , .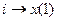

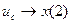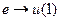Тоді наша система буде мати наступний вигляд:

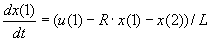
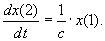
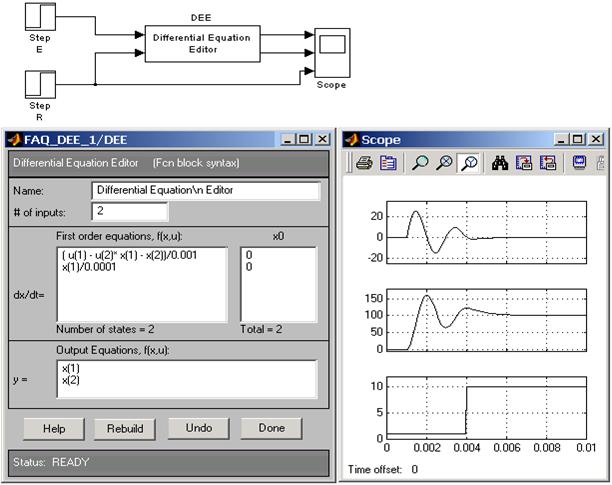
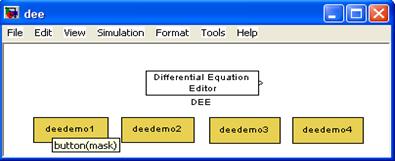Для цього наберемо у командному вікні команду >> dee, відкриється діалогове вікно:

Натиснувши кнопку відкриємо бібліотеки додатку Simulink. Відкриємо нове вікно Model і перетягнемо на нього блок Differential Equation Editor з вікна dee, далі, що б відкрити блок Differential Equation Editor необхідно на ньому двічі «клікнути» лівою клавішею миші.

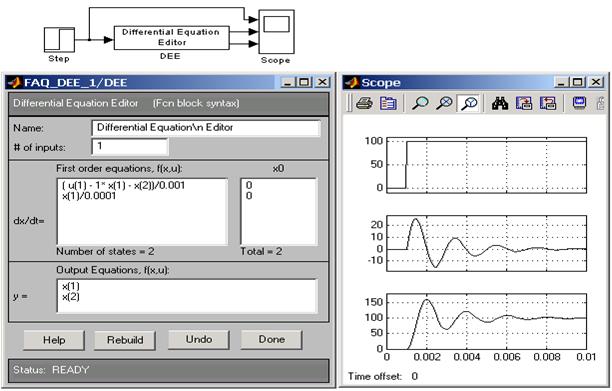
У вікні “# jf inputs” (кількість входів) поставимо 1 – у нас одна вхідна змінна 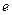. У вікні 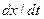запишемо систему рівнянь і у правому віконці “ 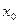” задамо відповідні початкові значення. У нижньому вікні “ 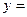” визначаємо вихідні параметри і натискаємо клавішу Done і закриваємо блок. Далі в якості значень вхідного параметра 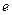задамо ступінчасту функцію Step і для виводу розв’язку на графік поставимо блок Scope (представлення графіку від часу). Двічі «клікнувши» на блок Scope, відкриємо його і натиснемо на клавішу , відкриється діалогове вікно де у віконці “Number of axes” поставимо 3 (три входи до блоку), що дозволить в одному вікні вивести три графіки. Зєднаємо всі блоки моделі стрілочками. Верхня стрілочка до блоку Scope, визначає, що перший графік буде представляти вхідний параметр 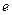, друга стрілочка – 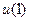, третя – 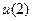. Після завершення побудови моделі запускаємо її на виконання натиснувши кнопку на головній панелі вікна моделі.

Можна ускладнити задачу, поклавши, що вхідний параметр R також представляє собою функцію у часі.

Завдання 6 а) Розв’язати диференційне рівняння з кроком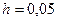

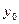
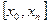
№	Рівняння			№	Рівняння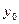

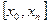
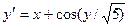
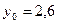
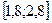
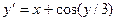
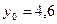
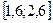
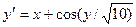
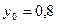
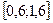
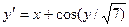
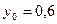
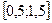
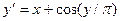
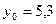
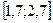
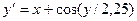
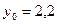
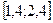
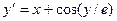
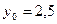
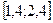
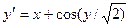
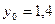
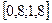
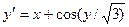
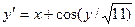
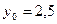
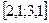
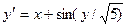
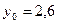
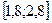
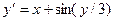
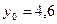
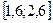
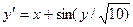
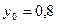
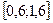
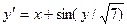
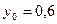
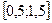
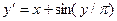
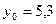
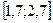
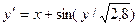
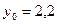
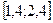
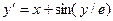
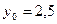
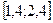
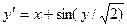
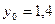
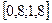
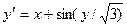
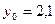
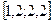
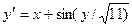
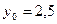
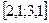
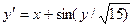
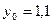
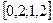
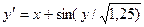
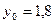
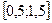
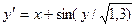
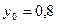
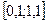
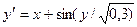
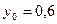
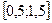
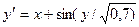
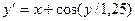
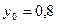
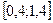
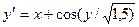
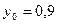
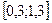
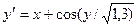
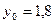
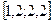
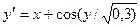
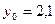
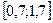
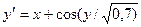
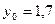
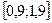
б) Розв’язати диференційне рівняння з кроком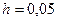

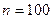
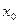
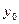
№	Рівняння				№	Рівняння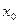
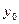
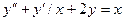
		0,7	0,5	0,2			0,9		-0,3
								0,1
		0,5
									0,2
								0,2
				0,5
								0,5