Типова задача. Задача 4.1. В результаті експериментальних вимірювань отримані наступні значення:

Задача 4.1. В результаті експериментальних вимірювань отримані наступні значення:

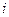
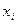
			-1
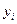
	4,1		4,7	5,9	2,4	3,6	5,2	4,3

Оцінити та побудувати функцію найкращого середньоквадратичного наближення.

Розв’язок. Mathcad.

Занесемо дані у таблицю (Вставка → Дані → Таблиця), назвавши її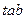

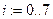змінна для нумерації елементів

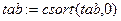впорядкуємо матрицю 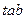за зростання значень першого стовпчика.

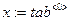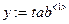, виділимо вектор аргументів та значень функції

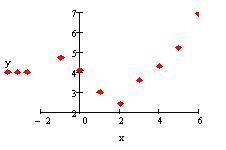Нанесемо точки заданої функції на координатну площину. З розташування точок очевидно, що на заданому відрізку краще застосовувати поліноміальне наближення.

Визначимо оптимальну степінь поліному. Для цього побудуємо таблицю скінченних різниць:

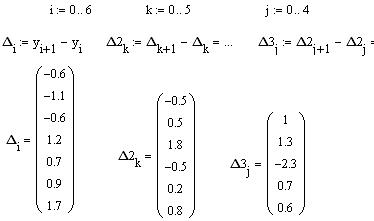Із значень скінченних різниць видно, що різниця третього порядку вже не зменшує, а збільшує значення, отже оптимальною стелінню полінома буде друга степінь. Збільшення степені може не покращити наближення. А привести до збільшення похибки.

Знайдемо коефіцієнти наближення поліномом 2-го порядку:

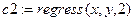- коефіцієнти поліному 2-го порядку

Функція 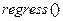повертає вектор-стовпчик значення коефіцієнтів, починаючи з 3-го елементу (перші три значення –службова інформація для функції 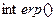). Переглянемо значення коефіцієнтів вирізавши тільки необхідну інформацію:

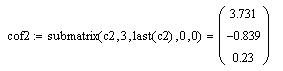
Побудуємо апроксимуючий поліном і задамо діапазон зміни аргументу:

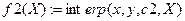
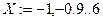
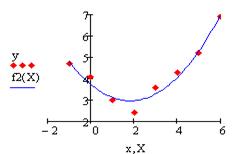Виведемо початкові точки та наближення на графік:

Оцінимо середньоквадратичну похибку наближення:

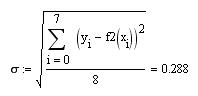
MATLAB. Нехай таблично задана функція із значеннями:

>> x = [0.1 0.3 0.45 0.5 0.79 1.1 1.89 2.4 2.45];>> y = [-3 -1 0.9 2.4 2.5 1.9 0.1 -1.3 -2.6];Будемо наближати її поліномами 1-ї. 3-ї та 5-ї степені:>> p1 = polyfit(x, y, 1)p1 = -0.6191 0.6755>> p3 = polyfit(x, y, 3)p3 = 2.2872 -12.1553 17.0969 -4.5273>> p5 = polyfit(x, y, 5)p5 = -6.0193 33.9475 -62.4220 35.9698 4.7121 -3.8631Отже ми отримаємо поліноми: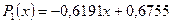

.

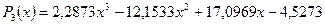
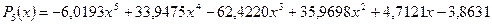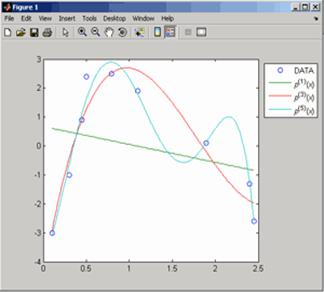Дя побудови графіків цих наближень необхідно знайти значення у точках на проміжку 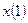до 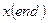ю Згенеруємо 100 точок за допомогою функції :

>> xx = linspace(x(1), x(end), 100);Обчислимо в них значення наших поліномів: >> yy1 = polyval(p1, xx); >>yy3 = polyval(p3, xx); yy5 = polyval(p5, xx);Побудуємо графіки:>> plot(x, y, 'o', xx, yy1, xx, yy3, xx, yy5).Що б оцінити похибку наближення функцію polyfit() необхідно викликати з двома вихідними аргументами: >> [p3, S3] = polyfit(x, y, 3), деp3 – коефіцієнти поліному: p3 = 2.2872 -12.1553 17.0969 -4.5273;S3 – інформація про наближення:S3 = R: [4x4 double]df: 5normr: 1.7201 – значення середньоквадратичної похибки. Задача 4.1. 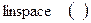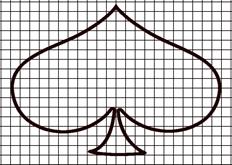Побудувати кубічний сплайн контуру фігури, зображеної на рисунку

Розв’язок. Проведемо аналіз заданої фігури:

1) вона симетрична відносно осі ординат, отже вісь 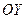можна провести посередині фігури, побудувати її для додатних 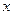і представити як .

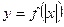2) 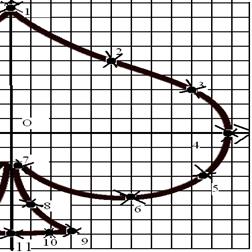Для кожного значення аргументу функції може існувати лише одне значення функції, отже проведемо вісь 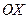у крайніх горизонтальних точках фігури.

Для побудови наближення необхідно визначити вузлові точки побудувати їх таблицю.

Наближення будемо будувати 4 сплайнами:

sp1 – точки1-4; sp2 – точки7-4; sp3 – точки7-9; sp4 – точки10-11.

(На кожному відрізку повинно буди не менше 3-х точок)

Складемо розрахункову таблицю координат опорних точок

х					х					х				х
у					у	-2	-4.2	-2,6		у	-2	-5	-7	у	-7.2	-7,05	-7