 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Построение интерполяционного многочлена Лагранжа
|
|
Наиболее простой и (для многих случаев) удобной является система функций 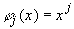 ,
,  . Функция
. Функция  при этом представляет собой многочлен степени
при этом представляет собой многочлен степени 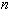 (интерполяционный многочлен) с коэффициентами
(интерполяционный многочлен) с коэффициентами  .
.
Система уравнений (3) в этом случае имеет вид:
 ,
,  (5)
(5)
Определителем этой системы является отличный от нуля определитель Вандермонда: 
Отсюда следует, что интерполяционный многочлен существует и единственен.
Непосредственное решение системы (5) для нахождения aj уже при небольших n приводит к сильному искажению значений aj. Получим явный вид нтерполяционного многочлена  , не решая систему (5).
, не решая систему (5).
Если  многочлен степени n такой что
многочлен степени n такой что  , то
, то 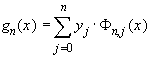 - искомый интерполяционный многочлен степени
- искомый интерполяционный многочлен степени 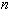 , т.к.
, т.к.  .
.
Так как  при
при  , то
, то  делится на
делится на  для любых
для любых  , то есть
, то есть
 . Так как
. Так как  , то
, то  .
.
Таким образом,
 (6)
(6)
Такая форма записи интерполяционного многочлена называется многочленом Лагранжа и обозначается, как правило,  .
.
Существуют и другие формы записи того же самого интерполяционного многочлена.
Если обозначить  , то
, то
 .
.
Тогда (6) можно записать в виде 
Дата публикования: 2014-11-18; Прочитано: 371 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
