 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
2 страница. а) при каких значениях и векторы компланарны;
|
|
Найти:
а) при каких значениях  и векторы
и векторы  компланарны;
компланарны;
б) длину и направляющие косинусы вектора  ;
;
в) вектор  , который перпендикулярен векторам
, который перпендикулярен векторам  .
.
№ 4. Даны векторы:  и число
и число  .
.
Вычислить:
а) скалярное произведение векторов  ;
;
б) модуль векторного произведения  ;
;
в) работу, совершаемую силой  на пути
на пути  ;
;
г) проекцию вектора  на вектор
на вектор  ;
;
д) площадь треугольника, построенного на векторах  , если начало вектора
, если начало вектора  помещено
помещено
в конец вектора  .
.
№ 5. Даны координаты вершин пирамиды A1 A2 A3 A4 : A1 (0, –1, –1), A2 (–2, 3, 5),
A3 (1, –5, –9), A4 (–1, –6, 3). Найти:
а)  ; б) площадь грани A1 A2 A3; в)
; б) площадь грани A1 A2 A3; в) 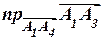 ;
;
г)  ; д) объём пирамиды.
; д) объём пирамиды.
№ 6. Найти проекцию вектора  на ось, определяемую вектором
на ось, определяемую вектором  , если
, если
 и
и  заданы разложением по взаимно перпендикулярным ортам
заданы разложением по взаимно перпендикулярным ортам 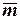 и
и  .
.
№ 7. Найти неизвестную координату вектора  , если
, если  составляет острый угол с осью,
составляет острый угол с осью,
одноименной неизвестной координате, и задан модуль вектора  .
.
№ 8. Найти модуль вектора  , если
, если  .
.
№ 9. Задан вектор силы  и координаты точек: т. A (2, 3, 4) и т. B (3, 1, –1).
и координаты точек: т. A (2, 3, 4) и т. B (3, 1, –1).
Найти:
а) работу заданной силы  по перемещению тела из точки A в точку B;
по перемещению тела из точки A в точку B;
б) модуль момента силы  , приложенной в точке A, относительно точки B.
, приложенной в точке A, относительно точки B.
№ 10. Вычислить проекции вектора  на оси координат, если A (0, –3, 6),
на оси координат, если A (0, –3, 6),
B (–12, –3, –3), C (–9, –3, –6).
ТИПОВОЙ РАСЧЁТ ПО ВЕКТОРНОЙ АЛГЕБРЕ
Вариант № 7
№ 1. Найти разложение вектора  по векторам:
по векторам:
 .
.
№ 2. Проверить, коллинеарны ли векторы  , если
, если
 .
.
№ 3. Даны векторы:  и число
и число  .
.
Найти:
а) при каких значениях  и векторы
и векторы  компланарны;
компланарны;
б) длину и направляющие косинусы вектора  ;
;
в) вектор  , который перпендикулярен векторам
, который перпендикулярен векторам  .
.
№ 4. Даны векторы:  и число
и число  .
.
Вычислить:
а) скалярное произведение векторов  ;
;
б) модуль векторного произведения  ;
;
в) работу, совершаемую силой  на пути
на пути  ;
;
г) проекцию вектора  на вектор
на вектор  ;
;
д) площадь треугольника, построенного на векторах  , если начало вектора
, если начало вектора  помещено
помещено
в конец вектора  .
.
№ 5. Даны координаты вершин пирамиды A1 A2 A3 A4 : A1 (5, 2, 0), A2 (2, 5, 0), A3 (1, 2, 4),
A4 (–1, 1, 1). Найти:
а)  ; б) площадь грани A1 A2 A3; в)
; б) площадь грани A1 A2 A3; в) 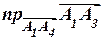 ;
;
г)  ; д) объём пирамиды.
; д) объём пирамиды.
№ 6. Найти проекцию вектора  на ось, определяемую вектором
на ось, определяемую вектором  , если
, если
 и
и  заданы разложением по взаимно перпендикулярным ортам
заданы разложением по взаимно перпендикулярным ортам 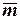 и
и  .
.
№ 7. Найти неизвестную координату вектора  , если
, если  составляет острый угол с осью,
составляет острый угол с осью,
одноименной неизвестной координате, и задан модуль вектора  .
.
№ 8. Найти модуль вектора  , если
, если  .
.
№ 9. Задан вектор силы  и координаты точек: т. A (–1, 1, –1) и т. B (1, 2, 2).
и координаты точек: т. A (–1, 1, –1) и т. B (1, 2, 2).
Найти:
а) работу заданной силы  по перемещению тела из точки A в точку B;
по перемещению тела из точки A в точку B;
б) модуль момента силы  , приложенной в точке A, относительно точки B.
, приложенной в точке A, относительно точки B.
№ 10. Вычислить проекции вектора  на оси координат, если A (3, 3, 1),
на оси координат, если A (3, 3, 1),
B (5, 5, –2), C (4, 1, 1).
ТИПОВОЙ РАСЧЁТ ПО ВЕКТОРНОЙ АЛГЕБРЕ
Вариант № 8
№ 1. Найти разложение вектора  по векторам:
по векторам:
 .
.
№ 2. Проверить, коллинеарны ли векторы  , если
, если
 .
.
№ 3. Даны векторы:  и число
и число  .
.
Найти:
а) при каких значениях  и векторы
и векторы  компланарны;
компланарны;
б) длину и направляющие косинусы вектора  ;
;
в) вектор  , который перпендикулярен векторам
, который перпендикулярен векторам  .
.
№ 4. Даны векторы:  и число
и число  .
.
Вычислить:
а) скалярное произведение векторов  ;
;
б) модуль векторного произведения  ;
;
в) работу, совершаемую силой  на пути
на пути  ;
;
г) проекцию вектора  на вектор
на вектор  ;
;
д) площадь треугольника, построенного на векторах  , если начало вектора
, если начало вектора  помещено
помещено
в конец вектора  .
.
№ 5. Даны координаты вершин пирамиды A1 A2 A3 A4 : A1 (2, –1, –2), A2 (1, 2, 1), A3 (5, 0, –6),
A4 (–10, 9, –7). Найти:
а)  ; б) площадь грани A1 A2 A3; в)
; б) площадь грани A1 A2 A3; в) 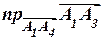 ;
;
г)  ; д) объём пирамиды.
; д) объём пирамиды.
№ 6. Найти проекцию вектора  на ось, определяемую вектором
на ось, определяемую вектором  , если
, если
 и
и  заданы разложением по взаимно перпендикулярным ортам
заданы разложением по взаимно перпендикулярным ортам 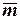 и
и  .
.
№ 7. Найти неизвестную координату вектора  , если
, если  составляет острый угол с осью,
составляет острый угол с осью,
одноименной неизвестной координате, и задан модуль вектора  .
.
№ 8. Найти модуль вектора  , если
, если  .
.
№ 9. Задан вектор силы  и координаты точек: т. A (3, 2, 1) и т. B (2, 3, 4).
и координаты точек: т. A (3, 2, 1) и т. B (2, 3, 4).
Найти:
а) работу заданной силы  по перемещению тела из точки A в точку B;
по перемещению тела из точки A в точку B;
б) модуль момента силы  , приложенной в точке A, относительно точки B.
, приложенной в точке A, относительно точки B.
№ 10. Вычислить проекции вектора  на оси координат, если A (–1, 2, –3),
на оси координат, если A (–1, 2, –3),
B (3, 4, –6), C (1, 1, –1).
ТИПОВОЙ РАСЧЁТ ПО ВЕКТОРНОЙ АЛГЕБРЕ
Вариант № 9
№ 1. Найти разложение вектора  по векторам:
по векторам:
 .
.
№ 2. Проверить, коллинеарны ли векторы  , если
, если
 .
.
№ 3. Даны векторы:  и число
и число  .
.
Найти:
а) при каких значениях  и векторы
и векторы  компланарны;
компланарны;
б) длину и направляющие косинусы вектора  ;
;
в) вектор  , который перпендикулярен векторам
, который перпендикулярен векторам  .
.
№ 4. Даны векторы:  и число
и число  .
.
Вычислить:
а) скалярное произведение векторов  ;
;
б) модуль векторного произведения  ;
;
в) работу, совершаемую силой  на пути
на пути  ;
;
г) проекцию вектора  на вектор
на вектор  ;
;
д) площадь треугольника, построенного на векторах  , если начало вектора
, если начало вектора  помещено
помещено
в конец вектора  .
.
№ 5. Даны координаты вершин пирамиды A1 A2 A3 A4 : A1 (–2, 0, –4), A2 (–1, 7, 1),
A3 (4, –8, –4), A4 (1, –4, 6). Найти:
а)  ; б) площадь грани A1 A2 A3; в)
; б) площадь грани A1 A2 A3; в) 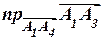 ;
;
г)  ; д) объём пирамиды.
; д) объём пирамиды.
№ 6. Найти проекцию вектора  на ось, определяемую вектором
на ось, определяемую вектором  , если
, если
 и
и  заданы разложением по взаимно перпендикулярным ортам
заданы разложением по взаимно перпендикулярным ортам 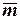 и
и  .
.
№ 7. Найти неизвестную координату вектора  , если
, если  составляет острый угол с осью,
составляет острый угол с осью,
одноименной неизвестной координате, и задан модуль вектора  .
.
№ 8. Найти модуль вектора  , если
, если  .
.
№ 9. Задан вектор силы  и координаты точек: т. A (1, –2, 1) и т. B (1, 1, 1).
и координаты точек: т. A (1, –2, 1) и т. B (1, 1, 1).
Найти:
а) работу заданной силы  по перемещению тела из точки A в точку B;
по перемещению тела из точки A в точку B;
б) модуль момента силы  , приложенной в точке A, относительно точки B.
, приложенной в точке A, относительно точки B.
№ 10. Вычислить проекции вектора  на оси координат, если A (–4, –2, 0),
на оси координат, если A (–4, –2, 0),
B (–1, –2, –4), C (3, –2, 1).
ТИПОВОЙ РАСЧЁТ ПО ВЕКТОРНОЙ АЛГЕБРЕ
Вариант № 10
№ 1. Найти разложение вектора  по векторам:
по векторам:
 .
.
№ 2. Проверить, коллинеарны ли векторы  , если
, если
 .
.
№ 3. Даны векторы:  и число
и число  .
.
Найти:
а) при каких значениях  и векторы
и векторы  компланарны;
компланарны;
б) длину и направляющие косинусы вектора  ;
;
в) вектор  , который перпендикулярен векторам
, который перпендикулярен векторам  .
.
№ 4. Даны векторы:  и число
и число  .
.
Вычислить:
а) скалярное произведение векторов  ;
;
б) модуль векторного произведения  ;
;
в) работу, совершаемую силой  на пути
на пути  ;
;
г) проекцию вектора  на вектор
на вектор  ;
;
д) площадь треугольника, построенного на векторах  , если начало вектора
, если начало вектора  помещено
помещено
в конец вектора  .
.
№ 5. Даны координаты вершин пирамиды A1 A2 A3 A4: A1 (14, 4, 5), A2 (–5, –3, 2),
A3 (–2, –6, –3), A4 (–2, 2, –1). Найти:
а)  ; б) площадь грани A1 A2 A3; в)
; б) площадь грани A1 A2 A3; в) 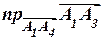 ;
;
г)  ; д) объём пирамиды.
; д) объём пирамиды.
№ 6. Найти проекцию вектора  на ось, определяемую вектором
на ось, определяемую вектором  , если
, если
 и
и  заданы разложением по взаимно перпендикулярным ортам
заданы разложением по взаимно перпендикулярным ортам 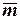 и
и  .
.
№ 7. Найти неизвестную координату вектора  , если
, если  составляет острый угол с осью,
составляет острый угол с осью,
одноименной неизвестной координате, и задан модуль вектора  .
.
№ 8. Найти модуль вектора  , если
, если  .
.
№ 9. Задан вектор силы  и координаты точек: т. A (–2, –1, 0) и т. B (5, 2, –1).
и координаты точек: т. A (–2, –1, 0) и т. B (5, 2, –1).
Найти:
а) работу заданной силы  по перемещению тела из точки A в точку B;
по перемещению тела из точки A в точку B;
б) модуль момента силы  , приложенной в точке A, относительно точки B.
, приложенной в точке A, относительно точки B.
№ 10. Вычислить проекции вектора  на оси координат, если A (5, 3, –1),
на оси координат, если A (5, 3, –1),
B (5, 2, 0), C (6, 4, –1).
ТИПОВОЙ РАСЧЁТ ПО ВЕКТОРНОЙ АЛГЕБРЕ
Вариант № 11
№ 1. Найти разложение вектора 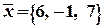 по векторам:
по векторам:
 .
.
№ 2. Проверить, коллинеарны ли векторы  , если
, если
 .
.
№ 3. Даны векторы:  и число
и число  .
.
Найти:
а) при каких значениях  и векторы
и векторы  компланарны;
компланарны;
б) длину и направляющие косинусы вектора  ;
;
в) вектор  , который перпендикулярен векторам
, который перпендикулярен векторам  .
.
№ 4. Даны векторы:  и число
и число  .
.
Вычислить:
а) скалярное произведение векторов  ;
;
б) модуль векторного произведения  ;
;
в) работу, совершаемую силой  на пути
на пути  ;
;
г) проекцию вектора  на вектор
на вектор  ;
;
д) площадь треугольника, построенного на векторах  , если начало вектора
, если начало вектора  помещено
помещено
в конец вектора  .
.
№ 5. Даны координаты вершин пирамиды A1 A2 A3 A4 : A1 (1, 2, 0), A2 (3, 0, –3), A3 (5, 2, 6),
A4 (8, 4, –9). Найти:
а)  ; б) площадь грани A1 A2 A3; в)
; б) площадь грани A1 A2 A3; в) 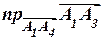 ;
;
г)  ; д) объём пирамиды.
; д) объём пирамиды.
№ 6. Найти проекцию вектора  на ось, определяемую вектором
на ось, определяемую вектором  , если
, если
 и
и  заданы разложением по взаимно перпендикулярным ортам
заданы разложением по взаимно перпендикулярным ортам 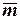 и
и  .
.
Дата публикования: 2014-11-18; Прочитано: 1035 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
