Среднее значение признака и методы вычисления этой величины

Полученные при обследовании значения признаков характеризуют каждую конкретную особь в отдельности. Общие свойства совокупности оценивают с помощью средней величины, которую обозначают в биометрии буквой M или 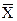. Этот показатель используется для характеристики однородных групп животных по какому-либо признаку, сравнения отдельных стад и пород, оценки предприятий, хозяйств и конкретных специалистов. Так, например, если в одном хозяйстве средний удой на корову составляет 3000 кг, а в другом - 4000 кг, то по среднему значению признака видно, где лучше стадо.

Различают несколько методов вычисления средней арифметической величины. Наиболее простой, который используют в основном для малых выборок - метод суммирования: складывают все значения вариант и делят их

сумму на объем выборки. В математическом выражении это выглядит так:

∑V где ∑ - знак суммирования,

M = ───; V - значения вариант,

n n - объем выборки.

Для примера найдем с помощью этого метода среднюю живую массу 10 гусей, кг: 5,6 7,0 6,3 7,4 8,0 6,7 6,4 6,9 6,1 6,8

5,6 + 7,0 + 6,3 + 7,4 + 8,0 + 6,7 + 6,4 + 6,9 + 6,1 + 6,8 67,1

M = ──────────────────────────────── = ─── = 6,71 кг.

10 10

В случаях, когда значения признака имеют разные частоты (вес) или в каждой группе уже известны средние показатели, среднюю арифметическую величину определяют методом взвешивания: каждое значение признака умножают на его частоту, полученные произведения суммируют и делят на объем выборки. Среднюю взвешенную величину вычисляют по формуле:

p₁V₁ + p₂V₂ + p_nV_n ∑рV где М - средняя взвешенная,

M = ───────────── = ────; p - частоты,

p₁ + p₂ + p_n ∑p V - варианты.

Для примера вычислим этим методом среднюю жирность молока коровы Зорьки за лактацию (табл.3).

3. Продуктивность коровы Зорька по месяцам лактации

Месяцы	Удой, кг (р)	Жирность молока, %	1% молоко, кг (рV)
Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь Январь	∑р = 4969	3,6 3,6 3,4 3,6 3,5 3,8 3,7 3,7 4,0 4,2	∑рV = 18156

В этом примере за конкретное значение признака (V) взят процент жира в молоке коров, а за частоту (р) - месячный удой.

∑рV 18155

M = ──── = ──── = 3,65(%)

∑р 4969

При группировке цифрового материала в вариационный ряд среднюю арифметическую величину удобно вычислять методом условных отклонений по формуле:

∑рa где A - условно среднее значение

M = A + i ────; i - классовый интервал

n р - частота, а - условное откл.

n - объем выборки

Используя этот метод, вычислим среднюю длину шерсти овец породы прекос по следующим данным: (см)

7,5 8,5 8,0 8,0 9,0 10,0 8,5 10,0 7,0 6,0 7,5 9,0 10,0 8,0

9,0 10,0 7,0 9,5 8,5 8,0 10,0 7,5 8,5 9,0 8,0 9,5 8,5 8,0

10,0 12,0 11,0 9,0 8,5 8,0 8,5 9,0 11,0 7,0 9,0 8,5

n = 40

Для построения вариационного ряда находим минимальное и макси-мальное значения признака, определяем лимит, устанавливаем число классов и величину классового промежутка.

1. min = 6,0; max = 12,0; lim = 12,0 - 6,0 = 6,0

2. Число классов - 6

lim 6,0

3. Классовый промежуток i = ────────── = ─── = 1,0 (см).

число классов 6

Схема расчета приведена в таблице 4.

4. Алгоритм вычисления средней арифметической величины методом условных отклонений

Границы классов (Vн. - Vк.)	Средние знач. класса (Vср.)	Частота (р)	Условные откл. (а)	р×а
6,0 – 6,9 7,0 – 7,9 А 8,0 – 8,9 9,0 – 9,9 10,0 – 10,9 11,0 – 12,0	6,5 7,5 8,5 9,5 10,5 11,5	n=40	-2 -1	-2 -6 ∑рa = 22

После построения вариационного ряда выделяем условно среднее значение признака - A. Обычно это среднее значение класса с максимальной частотой. В нашем примере A = 8,5. Затем проставляем условные отклонения (а), которые показывают, на сколько классовых промежутков каждый из классов отклоняется от условно среднего или нулевого класса. Вверх от нулевого идут отрицательные отклонения, вниз - положительные. После заполнения таблицы находим для каждого класса произведение частот (р) на отклонения (а) и их сумму (∑ра). Теперь по формуле находим среднее значение признака:

∑рa 22

М = A + i ───── = 8,5 + 1,0 ─── = 9,05 (см)

n 40

Кроме средней арифметической величины среднее значение признака характеризуют средняя геометрическая (G), средняя квадратическая (S), средняя гармоническая (H), мода (Мо) и медиана (Ме). Сведения об этих величинах и их использовании можно найти в специальной литературе по биометрии.