Теорема (о единственности разложения по данному базису)

Разложение любого вектора 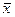по базису 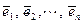является единственным.

Доказательство. Предположим, что для вектора 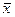наряду с разложением имеется другое разложение . Вычитая одно разложение из другого, получим равенство .

Поскольку базисные векторы линейно независимы, то из полученного равенства следуют равенства , что и доказывает теорему.

Следствие. Любые два вектора равны тогда и только тогда, когда равны их координаты в каком – либо базисе.

Таким образом, при фиксированном базисе линейного пространства каждый вектор однозначно определяется своими координатами в этом базисе.