Лабораторная работа №15. Нахождение собственных значений линейного оператора

Пусть А – квадратная матрица n-го порядка над полем К. Матрица

где l - независимая переменная, а Е – единичная матрица того же порядка, что и А, называется характеристической матрицей матрицы А.

Определитель характеристической матрицы

представляет собой полином (многочлен) n-ой степени от l и называется характеристическим полиномом матрицы А.

Легко видеть, что членом, имеющим относительно l степень n, будет только произведение элементов главной диагонали определителя |А-lЕ|. Все остальные члены характеристического определителя будут иметь относительно l степень не выше n-2, так как всякий член определителя |А-lЕ|, содержащий множителем элемент а_ij, не может содержать множителями элементы (а_ii-l) и (a_jj-l) и будет, следовательно, иметь относительно l степень не выше n -2.

В результате раскрытия скобок в члене определителя

(a ₁₁ - l) (a ₂₂ - l)... (a_nn -l)

получим не только l в степени n, но и l в степени n -1, при этом коэффициентом при l ⁿ будет (-1) ⁿ, а коэффициентом при l ^{n -1} – (-1) ^{n -1}(a ₁₁+ a ₂₂+...+ a_nn).

Сумма диагональных элементов матрицы А называется следом матрицы А и обозначается через Sp A, т.е.

Sp A = a ₁₁+ a ₂₂+...+ a_{nn .} (3).

Обозначим характеристический полином | А -l Е | через j(l). Тогда

j(l) = | А -l Е | = (-1) ⁿ l ⁿ + (-1) ^{n -1} (Sp A) l ^{n -1}+...+ p_n,

где p_n =j(0)= | А |.

Уравнение j(l) =0, или | А -l Е |=0 называется характеристическим, или вековым уравнением матрицы А. Корни характеристического уравнения матрицы А называются собственными значениями или характеристическими числами матрицы А. Совокупность всех собственных значений l₁, l₂,..., l _n, где каждое число фигурирует столько раз, какова его кратность как корня характеристического уравнения, называется спектром матрицы А.

Согласно формулам Виета произведение корней уравнения равно свободному члену, т.е.

l₁ l₂... l _n= | А |.

Отсюда следует, что матрица А тогда и только тогда имеет хотя бы одно собственное значение, равное нулю, когда она вырождена.

Для определения коэффициентов характеристического уравнения l⁴ -р₁ l³- р₂ l²- р₃ l- р₄ =0 матрицы, воспользуемся методом Леверрье, который заключается в следующем:

1) вычисляют степени матрицы А по формуле: А ^k = A ^k-1 * A (k =1, 2,..., n) (4);

2) находят след для каждой из матриц А ^k по формуле (3);

3) находят коэффициенты характеристического уравнения по формуле:

p_k = Sp А ^k - p ₁Sp А ^{k- 1}-... – p_{k -1} Sp А. (5),

в результате чего получаем характеристическое уравнение l ⁿ+р₁ l ^{n- 1}+ р₂ l ^{n- 2}+...+ р _{n- 1}l+ р _n =0 матрицы А.

Для нахождения корней характеристического уравнения воспользуемся методом Лобачевского, сущность которого заключается в квадрировании корней. При квадрировании корней каждый коэффициент преобразованного уравнения равен квадрату прежнего коэффициента, минус удвоенное произведение соседних с ним коэффициентов, плюс удвоенное произведение следующих в порядке близости к исходному коэффициентов (если нужный коэффициент отсутствует, то он считается равным нулю). Формулу нахождения коэффициентов можно записать в следующем виде:

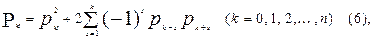
где предполагается р_s = 0 при s <0 и s > n.

Процесс квадрирования корней следует прекратить, если коэффициенты некоторого преобразованного уравнения в пределах точности вычислений равны квадратам соответствующих коэффициентов последующего преобразованного уравнения за счёт отсутствия удвоенных произведений. Корни уравнения находят по формуле:

(k =1, 2,..., n) (7),

где m – число квадрирований.

Пусть нам дана матрица 4–го порядка, имеющая следующий вид:

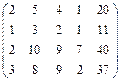
Приступим к реализации поставленной задачи, используя инструменты программы Excel. Для этого:

1. Включите компьютер.

2. После того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно Microsoft Excel.

· Заполните ячейки А1¸D4 таблицы значениями элементов матрицы.

3. Далее посчитаем степени матрицы А по формуле (4), т.е. найдём А ², А ³, А ⁴:

· выделите область А7¸D10;

· воспользуйтесь функцией МУМНОЖ, которая находится в мастере функций ƒ_х в категории МАТЕМАТИЧЕСКИЕ, где для нахождения матрицы А ² окне Массив1 выделите область А1: D4, и в окне Массив2 выберите область А1: D4;

·одновременно нажмите следующую комбинацию клавиш: Shift+Ctrl+Enter.

·

Рис. 12.1

для нахождения матрицы А ³ выделите область А12¸D15, снова воспользуйтесь функцией МУМНОЖ, где в окне Массив1 выделите область А7: D10, а в окне Массив2 выберите область А1: D4, после чего снова нажмите одновременно на клавиши Shift+Ctrl+Enter.

·аналогично найдите матрицу А ⁴в области А17¸D20, где в окне Массив1 выделите область А12: D15, а в окне Массив2 выберите область А1: D4, и после нажатия клавиш Shift+Ctrl+Enter экран Excel примет вид (см. рис. 12.1).

4. Найдём следы Sp А ^k для каждой из матриц А ^k по формуле (3). Для этого:

·в ячейку Е5 занесём формулу (3) , после чего нажмём на клавишу Enter; в результате Sp А =16.

·в ячейку Е11 занесём формулу вида: , после чего снова нажмём на клавишу Enter; в результате Sp А ²=312;

·в ячейках Е16 и Е21 подсчитаем Sp А ³ и Sp А ⁴ соответственно, в результате чего Sp А ³=5227, Sp А ⁴=91244.

5. Найдём коэффициенты р ₁, р ₂, р ₃ и р ₄ характеристического уравнения по формуле (5), где р ₁= - Sp А;

р ₂= (Sp А ²+ р ₁Sp А)/(-2);

р ₃= (Sp А ³+ р ₁Sp А ²+ р ₂Sp А)/(-3);

р ₄= (Sp А ⁴+ р ₁Sp А ³+ р ₂Sp А ²+ р ₃Sp А)/(-4).

Как видно из рис. 12.2, р ₁= -16, р ₂= -28, р ₃=71 и р ₄= -3, в результате чего получаем характеристическое уравнение, имеющее следующий вид:

l⁴ - 16l³ - 28l²+71l -3=0.

6. Найдём корни характеристического уравнения, пользуясь методом Лобачевского. Для этого составим таблицу, в первом столбце которой будут стоять степени, а в последующих пяти столбцах методом Лобачевского будут высчитываться коэффициенты преобразованных уравнений по формуле (6), в частности для коэффициентов Р₀, Р₁, Р₂, Р₃ и Р₄ получаем формулы:

Р _о= р _о²,

Р ₁= р ₁²-2 р ₁ р _о,

Р ₂= р ₂²-2 р ₁ р ₃+2 р _о р ₄,

Р ₃= р ₃²-2 р ₂ р ₄,

Р ₄= р ₄².

Для того чтобы реализовать поставленную задачу, надо:

· активизировать ячейку Н2 и занести в неё с клавиатуры число 1 (столбец Н – будет просчитывать степени);

·в ячейку I2 занесите с клавиатуры число 1 (столбец I – будет считать коэффициенты Р₀ преобразованных уравнений);

· в ячейках J2, K2, L2, M2 с клавиатуры занесите числа –16, -28, 71, -3 соответственно (столбцы J2, K2, L2, M2– будут считать коэффициенты Р₁, Р₂, Р₃, и Р₄ преобразованных уравнений);

· активизируйте ячейку Н3 и занесите в неё формулу вида =Н2*2, нажмите на клавишу Enter, после чего автозаполнением заполните ячейки Н4¸Н10;

·

Рис. 12.3

активизируйте ячейку I3 и занесите в неё формулу вида = I2*I2, нажмите на клавишу Enter, после чего автозаполнением заполните ячейки I4¸I10;

Аналогично предыдущим двум действиям, вначале заполните ячейки J3, K3, L3, M3 формулами вида: для J3: = J2*J2 -2*I2*К2, для К3: = К2*К2 -2*J2*L2 +2*I2*М2, для L3: = L2* L2 -2*К2*М2 и для М3: =М2*М2, после чего автозаполнением заполните ячейки J4¸ J10; К4¸К10; L4¸L10 и М4¸М10. Результаты вычислений представлены на рис. 12.3.

Из рис. 12.3 видно, что в ячейках J10, К10 и L10 вместо чисел появилось значение ошибки #ЧИСЛО!, что в конкретном случае указывает на то, что процесс квадрирования корней следует прекратить, так как коэффициенты преобразованного уравнения в пределах точности вычислений равны квадратам соответствующих коэффициентов последующего преобразованного уравнения за счёт отсутствия удвоенных произведений. Следовательно, ячейки Н10¸М10 очистим.

Посчитаем в ячейках J11 , К11 ; L11 и М11 . Получаем следующие значения (см. рис. 12.4).

Далее, логарифмируя полученные значения, найдём l₁, l₂, l₃ и l₄. Для этого:

· активизируйте ячейку J12;

·

Рис. 12.4

воспользуемся функцией СТЕПЕНЬ, которая находится в мастере функций ƒ_х в категории МАТЕМАТИЧЕСКИЕ, для того, чтобы посчитать l₁;

· в окне Число запишите число 10, а в окне Степень нажатием ЛКМ выделите ячейку J11, после чего нажмите на клавишу Enter (рис. 12.5);

· автозаполнением заполните ячейки К12¸М12.

7. Непосредственной подстановкой найденных корней в исходное уравнение, определим знаки корней. Для этого:

· активизируйте ячейку J14 и занесите в неё формулу:

·

Рис. 12.5

=I2*СТЕПЕНЬ(J12;4)+J2*СТЕПЕНЬ(J12;3)+K2*СТЕПЕНЬ(J12;2)+L2*J12+M2;

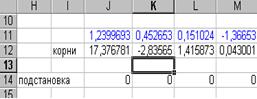
· заполните ячейки К14¸М14, используя предыдущую формулу, меняя лишь корни в функции СТЕПЕНЬ. В результате получим (рис. 12.6).

·В ячейке К14 значение уравнения равно –372, следовательно, поменяем знак в ячейке К12 на – противоположный, получаем, см. рис. 12.7:

Рис. 12.8

Рис. 12.6