Домашнее задание №3

«Дифференциальное и интегральное исчисление»

Задача 1. Чему равна сума правой и левой производных функции в точке

Решение. Данная функция не имеет производной в точке . Поэтому в этом случае, вообще говоря, техника дифференцирования не может быть использована. Вычислим односторонние производные в заданной точке непосредственно, пользуясь соответствующими определениями.

Левая производная функции в точке 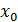определяется формулой

а правая производная функции в точке 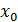определяется формулой

Вычислим значение левой производной функции в точке .

Вычислим значение правой производной функции в точке

Таким образом, сумма односторонних производных равна .

Задача 2. Чуму равен предел ?

Решение. Здесь имеем неопределенность вида . Подобного рода пределы можно вычислить с помощью первого замечательного предела и его следствий. При этом удобно применять эквивалентные бесконечно малые функции:

Задача 3. Чему равна производная функции ?

Ответ:

Задача 4. Чему равна производная первого порядка функции ?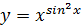

Ответ:

Задача 5. Определить чему равен предел .

Ответ: -9

Задача 6. Чему равно приближённое значение числового выражения , вычисленное с помощью полного дифференциала 1-го порядка функции двух переменных?

Ответ: 1,2

Задача 7. Чему равен полный дифференциал первого порядка функции ?

Ответ:

Задача 8. Чему равна производная функции ?

Ответ:

Задача 9. Чему равна производная функции ?

Ответ:

Задача 10. Если фигура ограничена графиком функции 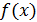(сверху) и (снизу), прямыми и , то её площадь (рис. 19)

Для доказательства перенесем параллельно оси ординат фигуру вверх на расстояние так, чтобы она оказалась выше оси абсцисс (рис. 20). После этого переноса её ограничивают графики функций и . При переносе площадь не меняется, и поэтому

Задача 11. Показать, что график непрерывно дифференцируемой на функции 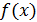имеет длину

Ответ:

Задача 12. Найти длину линии

Ответ:

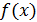Задача 13. На отрезке задана функция . Найти дифференциал линии , определяемой графиком данной функции.

Ответ:

Задача 14. Пусть задано тело с объемом , про которое известно следующее: имеется такая прямая - назовем её осью (рис. 23), что какую - бы плоскость, перпендикулярную оси , мы ни возьмем, нам известна площадь сечения рассматриваемого тела этой плоскостью.

Ответ:

Задача 15. Дана криволинейная трапеция, ограниченная графиком неотрицательной и непрерывной на отрезке функции 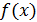. Трапеция опирается на этот отрезок, причем и вращается вокруг оси ординат. Найти объем получившегося тела вращения (рис. 24).

Ответ:

Задача 16. Найти неопределенный интеграл .

Ответ:

Задача 17. Найти интеграл .

Ответ:

Задача 18. Чему равен определённый интеграл: