Функция потерь

В стандартной множественной регрессии оценивание коэффициентов регрессии происходит “подбором” коэффициентов, минимизирующих дисперсию остатков (сумму квадратов остатков). Любые отклонения наблюдаемых величин от предсказанных означают некоторые потери в точности предсказаний, например, из-за случайного шума (ошибок). Поэтому можно сказать, что цель метода наименьших квадратов заключается в минимизации функции потерь. В этом случае, функция потерь определяется как сумма квадратов отклонений от предсказанных значений (термин функция потерь был впервые использован в работе Вальда - Wald, 1939). Когда эта функция достигает минимума, вы получаете те же оценки для параметров (свободного члена, коэффициентов регрессии), как, если бы мы использовали Множественную регрессию. Полученные оценки называются оценками по методу наименьших квадратов.

Мнк-оценкн, получающиеся в результате минимизации выбо­рочного критерия адекватности с квадратичной функцией по­терь, неустойчивы к нарушениям предположения о нормаль­ности распределения случайных ошибок. С утяжелением «хво­стов» распределения они быстро теряют свои оптимальные свой­ства. Это связано с тем, что квадратичная функ­ция потерь, используемая в мнк, придает слишком большой вес далеким отклонениям от регрессионной поверхности. Прогресс в области вычислительных методов позволяет перейти к использованию функций потерь 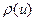, растущих при 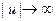более медленно, чем 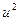. Соответствующие оценки по сравнению с мнк-оценками более устойчивы. Определенное внимание уделяется экспоненциально-взвешенным оценкам (эв-регрессии). Они допускают простую и наглядную интерпретацию, имеют хоро­шие выборочные свойства в случае небольших асимметричных искажений гауссовских распределений ошибок.

Функция потерь: , .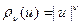

Параметры регрессионной поверхности находят из условия минимизации по вектору :

,

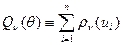где 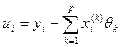. Покажем, что для :

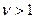1) решение этой задачи 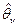единственно;

2) в модели 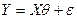для симметричных распределений случай­ных ошибок оценка 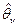состоятельна.

В самом деле, функция 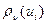, рассматриваемая как функция от , строго выпукла вниз. Следовательно, строго выпукла вниз и сумма 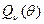, поэтому минимум 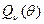единствен и достигается в одной точ­ке. Из строгой выпуклости 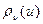и, следовательно, положи­тельности 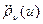вытекает, что для любой симметричной отно­сительно нуля случайной величины 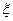для любого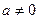

. (*)

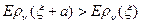Из закона больших чисел следует, что в моде­ли 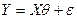для больших значений n для любого фиксированного вектора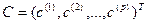

. (**)

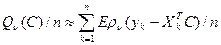При симметричном относительно нуля распределении слу­чайных ошибок, как следует из (*), правая часть (**) бу­дет наименьшей при 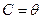. Следовательно, в силу (**), 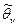должно быть при большом n близко к , т. е. оценка 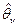состоя­тельная.