Общее назначение

Любой закон природы или общественного развития может быть выражен в конечном счете в виде описания характера или струк­туры взаимосвязей (зависимостей), существующих между изу­чаемыми явлениями или показателями (переменными величи­нами или просто переменными). Если эти зависимости:

а) стохастичны по своей природе, т. е. позволяют устанавливать лишь вероятностные логические соотношения между изучае­мыми событиями А и В, а именно соотношения типа «из факта осуществления события А следует, что событие В должно произойти, но не обязательно, а лишь с некоторой (как правило, близкой к единице) вероятностью Р»;

б) выявляются на основании статистического наблюдения за анализируемыми событиями или переменными, осуществляемого по выборке из интересующей нас генеральной совокупности,

то мы оказываемся в рамках проблемы статистического ис­следования зависимостей. Соответствующий математический аппарат, будучи таким образом нацеленным в первую очередь на решение основной проблемы естествознания: как по отдель­ным, частным наблюдениям выявить и описать интересующую нас общую закономерность? — занимает, бесспорно, централь­ное место во всем прикладном математическом анализе.

Условим­ся описывать функционирование изучаемого реального объек­та (системы, процесса, явления) набором переменных (рис. 1), среди которых:

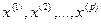— так называемые входные переменные, описывающие условия функционирования (часть из них, как правило, поддается регулированию или частичному управле­нию); в соответствующих математических моделях их назы­вают независимыми, факторами-аргументами, экзогенными, предикторными (или просто предикторами, т. е. предсказателя­ми), объясняющими;

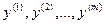— выходные переменные, характеризующие поведение или результат (эффективность) функционирования; в математических моделях их называют зависимыми, откликами, эндогенными, результирующими или объясняемыми;

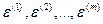— латентные (т. е. скрытые, не под­дающиеся непосредственному измерению) случайные достаточ­ные» компоненты, отражающие влияние (соответственно на 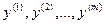) неучтенных на входе» факторов, а также случайные ошибки в измерении анализируемых показателей (в математических моделях их, как правило, именуют просто «остатками»).

рис.1. Общая схема взаимодействия переменных при статистическом исследовании зависимостей

Тогда общая задача статистического исследования зависи­мостей (в терминах изучаемых показателей) может быть сфор­мулирована следующим образом:

по результатам n измерений 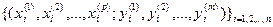исследуемых переменных на объектах (системах, процессах) анализируемой совокупности построить такую (векторнозначную) функцию

,

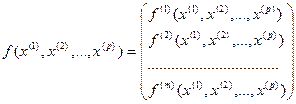которая позволила бы наилучшим (в определенном смысле) об­разом восстанавливать значения результирующих (прогнози­руемых) переменных 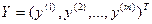по заданным зна­чениям объясняющих (предикторных) переменных .

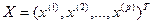Данная формулировка задачи нуждается в уточнениях. В частности, прежде всего мы должны ответить на следующие вопросы:

а) каково математическое выражение (или структура модели) искомой зависимости между X и Y, записанное в терминах X, Y, f(X) и ;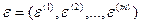

б) в соответствии с каким именно критерием качества аппроксимации значений Y с помощью функции f(X) мы будем определять наилучший способ восстановления значений ре­зультирующих показателей по заданным значениям объясняю­щих переменных?

в) с какой именно прикладной целью мы проводим все на­ше исследование, т. е. для решения каких конкретных задач собираемся использовать построенную в результате ис­следовании функцию f(X)?

Рассмотрим общую схему. Пусть значение исследуемого ре­зультирующего показателя 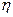при данных фиксированных величинах объясняющих переменных 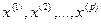случай­ным образом флюктуирует вокруг некоторого (вообще говоря, неизвестного) уровня 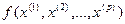, зависящего от кон­кретных значений предикторов 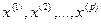, т. е. 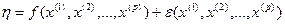, где остаточная компонента 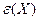определяет случайное откло­нение значения 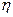от постоянного (при фиксированных 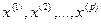) уровня f. При этом наличие флюктуации 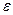может быть при­суще самой природе эксперимента или наблюдения, а может объясняться случайными ошибками в измерении величины f (тогда 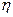является результатом несколь­ко искаженного измерения значения f). Когда говорят, что «не­которая величина (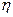) случайным образом флюктуирует вокруг определенного (неслучайного) уровня f», то, как правило, име­ют в виду, что среднее значение такой флюктуирующей слу­чайной величины должно быть равно f, т. е. 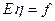. Посколь­ку условия эксперимента и, в частности, уровень, около кото­рого флюктуирует 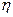, зависят от конкретных значений 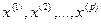некоторого набора объясняющих переменных, соответственн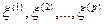о , то 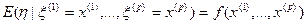. Функция 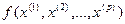, описывающая зависимость условного среднего значения 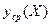результирующего показа­теля 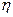(вычисленного при условии, что величины предсказы­вающих переменных зафиксированы на уровнях 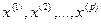) от заданных фиксированных значений предсказываю­щих переменных, называется функцией регрессии.

Происхождение термина «регрессия» (лат. «regression» — отступление, возврат к чему-либо) связано только с приклад­ной спецификой одного из первых конкретных примеров, в ко­тором это понятие было использовано, но никак не с его обще­смысловым наполнением. Этот термин был введен английским психологом и антропологом Ф. Гальтоном в связи с вопросом о наследственности роста. Обрабатывая статистические дан­ные, Гальтон нашел, что сыновья отцов, отклоняющихся по росту на л- дюймов от среднего роста всех отцов, сами отклоня­ются от среднего роста всех сыновей меньше, чем на х дюймов. Гальтон назвал выявленную тенденцию «регрессией к сред­нему состоянию» («regression to mediocrity»).

Иногда, при проведении анализа линейной модели, исследователь получает данные о ее неадекватности. В этом случае, его по-прежнему интересует зависимость между предикторными переменными и откликом, но для уточнения модели в ее уравнение добавляются некоторые нелинейные члены. Самым удобным способом оценивания параметров полученной регрессии является Нелинейное оценивание. Например, его можно использовать для уточнения зависимости между дозой и эффективностью лекарства, стажем работы и производительностью труда, стоимостью дома и временем, необходимым для его продажи и т.д. На самом деле Нелинейное оценивание можно считать обобщением методов множественной регрессии и дисперсионного анализа. Так, в методе множественной регрессии (и в дисперсионном анализе) предполагается, что зависимость отклика от предикторных переменных линейна. Нелинейное оценивание оставляет выбор характера зависимости за вами. Например, вы можете определить зависимую переменную как логарифмическую функцию от предикторной переменной, как степенную функцию, или как любую другую композицию элементарных функций от предикторов.

Если позволить рассмотрение любого типа зависимости между предикторами и переменной отклика, возникают два вопроса. Во-первых, как истолковать найденную зависимость в виде простых практических рекомендаций. С этой точки зрения линейная зависимость очень удобна, так как позволяет дать простое пояснение: “чем больше x (т.е., чем больше цена дома), тем больше y (тем больше времени нужно, чтобы его продать); и, задавая конкретные приращения x, можно ожидать пропорциональное приращение y ”. Нелинейные соотношения обычно нельзя так просто проинтерпретировать и выразить словами. Второй вопрос - как проверить, имеется ли на самом деле предсказанная нелинейная зависимость.