Однокристальна реалізація на ПЛІС алгоритму швидкого перетворення Фур'є

Задача виконання ШПФ за мінімальний час є досить актуальною при побудові швидкодіючих систем спектрального аналізу задач виявлення, цифрової фільтрації в частотній області і т.д..

В даний час існує досить багато реалізацій алгоритму ШПФ на замовлених НВІС і процесорах ЦОС, однак реалізація алгоритму на ПЛІС дозволяє створити найбільш оптимальні архітектурні рішення з максимальною продуктивністю для сучасного технологічного рівня НВІС.

Обчислення прямого ДПФ у загальному випадку робиться по наступному виразу:

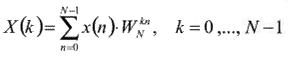
, (1)

де x(n) - послідовність з N часових відліків;

X(k) - послідовність з N частотних відліків;

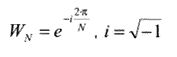
Обчислення безпосередньо по формулі (1) вимагає дуже великого числа операцій: приблизно N² операцій множення і N² операцій додавання комплексних чисел. Алгоритми ШПФ дозволяють значно скоротити їхнє число.

Розглянемо алгоритм швидкого перетворення Фур'є з проріджуванням за часом. Якщо послідовність x(n) довжиною N = 2L, де L > 0, L - ціле, розділити на дві N/2 - точкові послідовності, що складаються з x(n) з парними і непарними номерами відповідно, то вираз для ДПФ можна записати у виді:

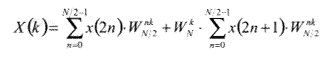k = 0,..., N - 1,

, (2)

де x(n) - послідовність з N часових відліків;

X(k) - послідовність з N частотних відліків;

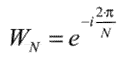— коефіцієнти перетворення,

де .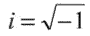

Кожна із сум у (2) є N/2-точковим ДПФ, що аналогічним чином можна представити через N/4-точкові, N/4- точкові через N/8-точкові і т.д., поки не залишаться тільки 2-точкові. Таких ступенів перетворення усього буде L = log2 N. На m-ступені відбувається перетворення безлічі N комплексних чисел Xm(n) у безліч N комплексних чисел Xm+1(n) відповідно до базової операції "метелик", описуваної виразами:

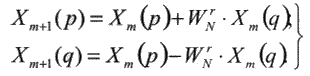
, (3)

На рис. 1 зображений спрямований граф, що реалізує алгоритм ШПФ для N = 8 із проріджуванням за часом.

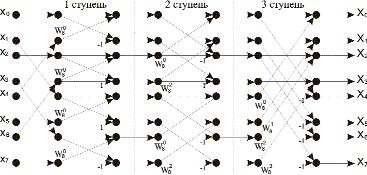
Рис. 1. Алгоритм ШПФ 8 точок із проріджуванням за часом

Процес обчислення повного перетворення можна умовно розбити на три кроки. На першому відбувається перетворення вхідної послідовності xn відповідно до двійкової інверсії номерів і наступним обчисленням першого часткового перетворення відповідно до виразу (3). На другому відбувається обчислення другого часткового перетворення, на третьому - повного перетворення Xn. Аналогічно для обчислення ШПФ 256 точок буде потрібно 8 кроків, 1024 точки - 10 кроків. Подібним чином можна представити ШПФ для будь-якого N = 2L, де L? > 0, L - ціле і дорівнює числу кроків.