Процес формування АЧХ

Для обчислення АЧХ нерекурсивних ЦФ здебільшого застосовують метод передаточних функцій. Від передаточної функції, яка в загальному вигляді записується як многочлен виду:

H(Z)= a ₀ + a₁Z^-1 +a₂Z^-2 + … + a_N-1Z^-(N-1),

можна перейти до комплексної частотної характеристики, підставляючи Z=e ^-jw, що відповідає перетворенню Фур’є

H(e ^jw)= 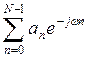= | H(e ^jw) | e^{arg[H(e^jw)]} (11.3)

де { a } – коефіцієнт фільтра N-го порядку; | H(e ^jw) | – АЧХ ЦФ; arg[H(e^jw) ] – фазо-частотна характеристика (ФЧХ).

Згідно з формулою Ейлера для комплексних чисел e ^jw= cos w + j sin w, перетворимо комплексну частотну характеристику ЦФ:

H(e ^jw)= + j .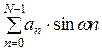

Звідси можна визначити АЧХ.

Можливий такий варіант обчислень: визначення дискретизованих АЧХ і ФЧХ як результату вагового сумування в узгодженому фільтрі дискретизованих значень потрібної для дослідження сітки гармонічних коливань з одиничною амплітудою і постійною початковою фазою:

u_si = sin 2pf_it; u_ci = cos 2pf_it,

де u_si i u_ci – ортогональні складові аналітичного сигналу u_i= exp(j2pf_it).

Результат проходження складових через узгоджений з сигналом фільтр – вихідна інформація для обчислення модуля (АЧХ) і аргумента (ФЧХ) коефіцієнта передачі. Згідно з алгоритмом u_{c вих і} визначається як сума зважених з відповідними коефіцієнтами { a } значень гармонійної одиничної напруги u­_ci в моменти часу, кратні періоду дискретизації Т:

u_{c вих і} = ,

де N - порядок фільтра, cos 2pf_ikT – фазовий коефіцієнт одиничної косинусної напруги. Його значення детерміноване і може зберігатися в запам’ятовуючому пристрої для реального каналу, якщо відомі сітка частот, період дискретизації аналізованої вхідної послідовності.

В загальному випадку, якщо фільтр N-го порядку,

u_{c вих і} = .

Аналогічно можна визначити реакцію фільтра на синусоїдальну вхідну напругу з нульовою початковою фазою:

u_{s вих і} = .

Для будь-якої з частот f_i можна визначити значення АЧХ і ФЧХ:

| k(f_i) | = ; f_i = arctg (u_si / u_ci) (11.4)

За отриманими результатами визначається АЧХ.

Розглянемо процедуру діагностики схеми ШПФ на прикладі системи опрацювання сигналів когерентно-імпульсної РЛС (див. рис.11.4), де для вимірювання доплерівської частоти використовується n каналів з погодженими фільтрами. Нехай процесор виконує N -точкове амплітудне дискретне перетворення Фур’є згідно з формулою (11.5)

, (11.5)

де N визначає розмірність перетворення, n -номер елемента віддалі, l – номер гармоніки, i -номер періоду повторення в межах інтервалу обчислення ДПФ, W(i) вагова функція.

Тоді на виході генератора тестових сигналів сигнал

, (11.6)

де, А - амплітуда сигналу, S - кількість частотних діапазонів між сусідніми l, Q – визначає смугу перевірки АЧХ (, де m, p - кількість гармонік, в діапазоні яких (відносно l) перевіряється АЧХ, , , s_i – біжуче значення частотного діапазону між сусідніми l).

Алгоритм формування вхідних даних полягає у видачі на кожному етапі обчислень синфазної і квадратурної складових комплексного сигналу, фаза яких визначається на значення Q на двох сусідніх періодах, на кожному з яких вираховується одне значення U(і).

Процедура діагностики відбувається таким чином. Для пристрою ШПФ задається значення гармоніки l_j. На інформаційні входи поступає вхідний сигнал . Зміна значень (синфазна і квадратурна складові) на вході процесора відбувається на кожному періоді повторення (по і). Одне значення визначається сумуванням по і (див.8.5). Після того змінюється частота поступлення , зміна задається значенням 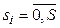, і вираховується наступне значення . Повна АЧХ, для заданого l_j, отримується після поступлення на вхід S*N значень вхідного сигналу. На практиці обмежуються перевіркою АЧХ для ±3 l, відносно l_j. Після перевірки амплітудно-частотних характеристик для всіх гармонік і елементів віддалі процес діагностики завершується. В ідеальному випадку характеристики всіх АЧХ повинні бути ідентичними.

Тобто, при використанні такого підходу процес діагностики пристрою ШПФ розбивається на три етапи:

- задання значень для отримання числової послідовності вхідних сигналів;

- визначення значень Y(n,l) реальної АЧХ;

- порівняння значень ідеальної і реальної АЧХ в кожній точці виміру.