Z-преобразования некоторых последовательностей

Единичный импульс

Т.к. при всех n, кроме n=0, где x(n)=1, 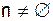, то:

X(z)=1

X(z) сходится на всей z-плоскости, т.к. единичный импульс является последовательностью конечной длины.

Единичный скачок

x(n)=0 везде, кроме , где x(n)=1, тогда:

Полученное выражение представляет собой геометрическую прогрессию. X(z) сходится при , т.к. X(z) имеет единственную особую точку (полюс).

0+j*1

0-j*0

Простая экспоненциальная последовательность

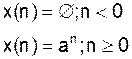
Особая точка:

z=a

X(z) – cходится при z=a<1.

Комплексная экспонента с единичной амплитудой.

X(z)=

Особая точка: 1-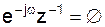

z=

Ряд X(z) – сходится, т.к. имеет только одну особую точку.

Комплексная экспонента с убывающей амплитудой.

Особые точки:

;

Это общий случай всех рассмотренных точек, расположенных на z-плоскости.

Соотношение между z-преобразованием и Фурье-преобразованием последовательности, о.с. при :

, что совпадает с преобразованием Фурье исходной последовательности.

На z-плоскости изображают как полюса (крестиками), так и нули функции X(z). Тогда можно восстановить исходную функцию X(z), зная расположение ее нулей z1, z2,… и полюсов p1, p2,…:

…

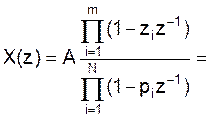после перемножений получим:

… , где А – произвольная постоянная (м.б. =1)

Полученное выражение часто используется при синтезе цифровых фильтров.