Билет 13

Геометрические характеристики плоских фигур - основные понятия.

Рассмотрим некоторое поперечное сечение в системе координат x, y

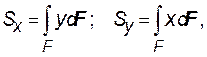
Первый интеграл называется статическим моментом сечения относительно оси x, а второй – статическим моментом сечения относительно оси y.

При параллельном переносе осей статический моменты изменяются. Искомые статические моменты будут равны.

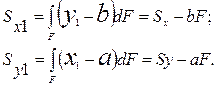(Определение положения ц.т. сложной фигуры: Yc= Sx/A,Xc=Sy/A)

При параллельном переносе осей статический момент изменяется на величину, равную произведению площади F на расстояние между осями.

О сь, относительно которой статический момент равен нулю, называется центральной.

Моменты инерции сечения

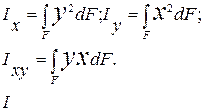
Первые 2 интеграла называются осевыми моментами инерции сечения относительно осей х и у соответственно. Третий интеграл называется центробежным моментом инерции сечения относительно х, у. Ось наз-ся главной, если J_XcYc=0. Ось наз-ся главной центральной, если S_X=0, S_Y=0, J_XcYc=0.

формулы преобразования моментов инерции при параллельном переносе осей.

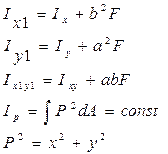
При параллельном переносе осей (если одна из осей – центральная) осевые моменты инерции изменяются на величину, равную произведению площади сечения на квадрат расстояния между осями.