 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
О т д е л е н и е к о р н е й
|
|
Пусть дано уравнение f(x)=0, в котором функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале а<x<в. Всякое значение z, обращающее функцию f(x) в нуль, т.е. такое, что f(z)=0, называется корнем уравнения. Для отделения корней полезна известная из математического анализа теорема Больцано-Коши:
Если непрерывная функция f(x) принимает значения разных знаков на концах отрезка (a,b),т.е. если f(a)  f(b) <0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x)=0,т.е. найдется хотя бы одно число z Î (a,b) такое, что f(z)=0.
f(b) <0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x)=0,т.е. найдется хотя бы одно число z Î (a,b) такое, что f(z)=0.
Процесс отделения корней начинается с установления знаков функции f(x) в граничных точках области существования функции. Затем определяются знаки функции f(x) в ряде промежуточных точек x= a 1, a2,... a 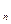 , выбор которых учитывает особенности функции f(x). Если окажется, что
, выбор которых учитывает особенности функции f(x). Если окажется, что
f(aк)  f(a к+1)<0, то в силу теоремы Больцано-Коши в интервале (a к,a к+1) имеется корень уравнения f(x)=0.
f(a к+1)<0, то в силу теоремы Больцано-Коши в интервале (a к,a к+1) имеется корень уравнения f(x)=0.
Если функция f(x) является многочленом n -ой степени, то эта функция определена в бесконечном интервале - ¥ < x<+ ¥. Для определения промежутка, в котором находится хотя бы один корень уравнения, придется вычислять значение функции f(x) в большом количестве промежуточных точек. Для сужения интервала, в котором следует проводить поиск корней алгебраических уравнений, можно воспользоваться следующей теоремой из высшей алгебры: для многочлена f(x) c любыми числовыми коэффициентами число C=1+Am/  (*) служит верхней границей для модулей всех его корней, включая комплексные, где
(*) служит верхней границей для модулей всех его корней, включая комплексные, где  - модуль коэффициента при x
- модуль коэффициента при x  , Am - максимальный модуль из остальных коэффициентов.
, Am - максимальный модуль из остальных коэффициентов.
П р и м е р 1. Найти интервал, внутри которого находятся корни многочлена f(x)= x  + 2 x
+ 2 x  - 5 x
- 5 x 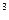 +8 x
+8 x  - 7 x - 3
- 7 x - 3
Для этого многочлена  =1, Am =8. Отсюда С=1+8/1=9,таким образом, все пять корней многочлена находятся внутри интервала [ -9, +9 ].
=1, Am =8. Отсюда С=1+8/1=9,таким образом, все пять корней многочлена находятся внутри интервала [ -9, +9 ].
Интервал, определяемый с помощью формулы (*), оказывается слишком большим, особенно для действительных корней. Чтобы уменьшить объем вычислений, были разработаны более точные, но и более сложные методы определения границ интервалов, содержащих действительные корни. Если вычисления проводить с помощью компьютера, то их объем большого значения не имеет, и потому нет необходимости рассматривать здесь иные методы определения границ интервалов.
П р и м е р 2. Отделить действительные корни многочлена, рассмотренного в примере 1: f (x)= х5 + 2 x4 - 5 x3 + 8 х2 - 7 x - 3.
Для решения этой задачи вычисляются значения полинома, приняв за начальное значение x  = - 9 и шаг изменения аргумента D x = 1. Результаты вычислений приведены в таблице 2.
= - 9 и шаг изменения аргумента D x = 1. Результаты вычислений приведены в таблице 2.
Т А Б Л И Ц А 2
| X | - 9 | - 8 | - 7 | - 6 | - 5 | - 4 | - 3 | - 2 |
| У | -39574 | -21451 | -9852 | - 1377 | -1018 | - 39 | + 144 | + 83 |
П р о д о л ж е н и е т а б л и ц ы 2
| Х | - 1 | + 1 | + 2 | + 3 | + 4 | + 5 | + 6 | |
| У | -3 | - 4 |
Из таблицы видно, что многочлен f(x) имеет по крайней мере три действительных корня: положительный 1 < x  < 2, так как f (1) <0, а f(2) >0, и два отрицательных - 1 < x
< 2, так как f (1) <0, а f(2) >0, и два отрицательных - 1 < x 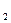 < 0
< 0
(f (- 1) = + 18, f (0) = - 3), - 4 < x 3 < -3 (f (- 4) = - 39, f (-3) = + 144).
Трансцендентные уравнения чрезвычайно разнообразны, поэтому отделение корней в них несколько сложнее. Для проведения этой операции приходится анализировать функцию f(x) и во многих случаях строить ее график, чтобы определять приближенно точки пересечения этого графика с осью абсцис. Часто бывает выгодно первоначальное уравнение f(x) = 0 заменять равносильным ему уравнением j (x) = y (x), где функции j (x) и y (x) - более простые, чем функция f(x). Тогда, построив графики функций у = j (x) и у = y (x), искомые корни получают как абсциссы точек пересечения этих графиков.
П р и м е р 3. Найти приближенное значение корня уравнения
x lg x - 1 = 0. (3)
Полагая x ¹ 0, разделим уравнение на x и запишем его в следующим виде: lg x= 1 / х. Отсюда видно, что j (x) = lg x, а y (x) = 1 / x, где
j (x) - логарифмическая кривая, а y (x) - гипербола. Решением уравнения (3) является абсцисса точки пересечения логарифмической кривой и гиперболы. Поскольку логарифмическая кривая при x < 0 не существует, то точку пересечения кривых j (x) и y (x) следует искать при x >0. 
Для построения кривой необходимо, как минимум, три точки. Найдем их для каждой кривой. За начальное значение x примем х=1, шаг изменения x для простоты вычислений принимается равным также единице. Вычисления приведены в табличной форме.
Та б л и ц а 3
|

Из таблицы 3 и рисунка видно, что корень уравнения (3) находится в интервале (2; 3).
П р и м е р 4. Найти приближенное значение корня уравнения
e 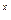 - x - 2 = 0 (4)
- x - 2 = 0 (4)
Перенося последние два члена уравнения в правую часть, получаем эквивалентное уравнение e 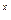 = x + 2. Из этого равенства видно, что корнем уравнения является абсцисса точки пересечения графика показательной функции j (x) = e
= x + 2. Из этого равенства видно, что корнем уравнения является абсцисса точки пересечения графика показательной функции j (x) = e 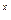 и прямой линии y (x) = x + 2.
и прямой линии y (x) = x + 2.
График показательной функции располагается над осью x при любых значениях x - положительных и отрицательных. Прямая же y (x) = x+ 2 располагается над осью x только при x>-2. При этих значениях x и следует искать точки пересечения графиков функций j (x) и y(x).За начальное значение аргумента обоих функций принимается x = -2. Шаг изменения x принимается равным единице.Вычисления значений функций j(x), y(x) и заданной функции f(x)=e 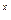 -х-2 проводятся в табличной форме.
-х-2 проводятся в табличной форме.
Та б л и ц а 4
| X | -2 | - 1 | + 1 | + 2 | |
e 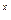
| 0,135 | 0, 368 | 2,72 | 7,39 | |
| X + 2 | |||||
| f (x) | 0,135 | - 0, 632 | - 1 | - 0,28 | +3,39 |
Из таблицы 4 видно, что графики функций j (x) и y (x) пересекаются в двух точках. Следовательно, уравнение (4) имеет два корня один из них расположен в интервале (- 2; - 1), второй- в интервале (1;2). Рассмотренные примеры позволяют сделать вывод,что отделение корней алгебраических и трансцендентных уравнений можно проводить по единому алгоритму:
1) назначается начальное значение аргумента x  и шаг его изменения D x;
и шаг его изменения D x;
2) вычисляются значения заданной функции f(x)в точках x  = x
= x  и
и
x 
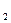
 = x
= x  +
+  x;
x;
3) находится произведение p = f(x 1) × f(x 2);
4) если p <0, то корень уравнения находится внутри интервала (x  ; x
; x 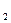 ), расчет окончен;
), расчет окончен;
5) если p >0,то принимается x  = x
= x  + Dx, x
+ Dx, x 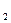 = x
= x  +Dx = x
+Dx = x  + 2 D x, и все действия начиная с п. 2, повторяются.
+ 2 D x, и все действия начиная с п. 2, повторяются.
Разница для алгебраических и трансцендентных уравнений заключается в том, что для алгебраических уравнений значение x  может быть вычислено по формуле (*), а для трансцендентных уравнений значение хо должно быть получено путем анализа заданной функции f (x).
может быть вычислено по формуле (*), а для трансцендентных уравнений значение хо должно быть получено путем анализа заданной функции f (x).
Рассмотренный алгоритм может быть реализован в виде подпрограммы на языке Ф О Р Т Р А Н. Как известно, в Ф О Р Т Р А Н е применяются подпрограммы двух видов: F U N C T I O N и S U B R O U T I N E. Подпрограмма F U N C T I O N употребляется в тех случаях, когда необходимо вычислять и передавать в вызывающую программную единицу единственное значение. В других случаях - S U B R O U T I N E.
В нашем случае подпрограмма должна выдать значения границ интервала, внутри которого содержится корень уравнения, и количество шагов, совершенных на пути к этому интервалу.Т.е. здесь может быть применена только подпрограмма типа S U B R O U T I N E. При «ручном» счете подсчет количества шагов не обязателен, но при расчете на компьютере он необходим.Дело в том, что при неудачном задании начального значения аргумента компьютер будет совершать шаг за шагом, не находя интервала, содержащего корень уравнения. И выйти из цикла, повторяющего п.п. 2 - 5 описанного выше алгоритма, самостоятельно он не сможет. В этом случае говорят, что «компьютер зациклился». Чтобы не произошло зацикливания, количество шагов должно быть ограничено некоторым достаточно большим числом, по достижении которого компьютер должен прекратить вычисления, выдав сообщение, что за оговоренное количество шагов интервал, содержащий корень уравнения, не найден. В этом случае оператор должен задать новое значение x  и снова запустить программу.
и снова запустить программу.
В подпрограмме должны неоднократно вычисляться значения функции
f(x).Чтобы подпрограмму не приспосабливать к каждому решаемому уравнению, вычисления функции f (x) должны проводиться путем вызова подпрограммы - функции F U N C T I O N F (x). И только эта подпрограмма должна быть написана заново для каждого решаемого уравнения. С учетом изложенного подпрограмма отделения корней нелинейных уравнений может иметь, например, вид, приведенный в приложении 1.
Дата публикования: 2014-11-18; Прочитано: 453 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
