 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Інтерполяційний многочлен Ньютона
|
|
Для побудови інтерполяційного многочлена Ньютона необхідно спочатку ввести поняття скінчених і розділених різниць. Нехай  – довільні попарно не рівні між собою вузли інтерполяції, в яких відомі значення функції
– довільні попарно не рівні між собою вузли інтерполяції, в яких відомі значення функції  .
.
Скінченими різницями першого порядку називають величини, що обчислюються за формулами:
 (23)
(23)
Скінченими різницями другого порядку називають:
 (24)
(24)
У загальному вигляді скінчені різниця  -го порядку обчислюється за формулою
-го порядку обчислюється за формулою
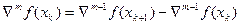 (25)
(25)
Розділені різниці першого порядку для  у вузлах інтерполяції мають вигляд:
у вузлах інтерполяції мають вигляд:
 (26)
(26)
Розділені різниці другого порядку записують у вигляді:
 (27)
(27)
Взагалі, якщо розділені різниці  -го порядку вже визначені, то розділені різниці
-го порядку вже визначені, то розділені різниці  -го порядку знаходяться за формулою
-го порядку знаходяться за формулою
 . (28)
. (28)
При обчислені розділених різниць прийнято записувати їх у вигляді таблиці
| x | f(x) | ∆ f(x) | ∆2 f(x) | ∆3 f(x) | … | ∆n f(x) |
| x0 | f(x0) | |||||
| x1 | f(x1) | f(x0; x1) | ||||
| x2 | f(x2) | f(x2; x1) | f(x0; x1; x2) | |||
| x3 | f(x3) | f(x3; x2) | f(x1; x2; x3) | f(x0; x1; x2; x3) | ||
| … | … | … | … | … | … | |
| xn | f(xn) | f(xn-1; xn) | f(xn-2; xn-1; xn) | f(xn-3; xn-2; xn-1; xn) | … | f(x0; x1; …; xn) |
Використовуючи розділені різниці, можна одержати формулу Ньютона для нерівних проміжків у вигляді:
 (29)
(29)
Зауважимо, що в обчисленнях за формулою (29) будуть брати участь тільки діагональні елементи таблиці, а всі інші елементи таблиці являються тільки проміжковими і потрібні тільки для обчислення діагональних елементів.
Переконаємось, що отриманий вираз дійсно є інтерполяційним многочленом, а саме він є многочленом 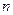 -го степеня і приймає у вузлах інтерполяції задані значення:
-го степеня і приймає у вузлах інтерполяції задані значення:


Вибравши довільну точку  , можна довести, що
, можна довести, що

тобто всі вимоги до інтерполяційних многочленів виконуються.
Приклад 4. Функцію  на відрізку
на відрізку  інтерполювати многочленом Ньютона 5-го степеня, обчислити його значення при
інтерполювати многочленом Ньютона 5-го степеня, обчислити його значення при  та порівняти одержане наближене значення із точним.
та порівняти одержане наближене значення із точним.
Розв’язання. Програма побудови матриці розділених різниць  , многочлен Ньютона
, многочлен Ньютона  та результати обчислень наведено на лістингу 4. З наведених
та результати обчислень наведено на лістингу 4. З наведених
результатів видно, що похибка 

На вигляд многочлен Ньютона відрізняється від многочлена Лагранжа. Але якщо ці многочлени побудовано для тієї самої функції і однієї й тієї самої системи вузлів, то за теоремою про єдиність розв’язку інтерполяційної задачі вони тотожно дорівнюватимуть одна одній, тобто  . А тому і залишковий член інтерполяційної формули Ньютона збігатиметься з залишковим член інтерполяційної формули Лагранжа. Отже,
. А тому і залишковий член інтерполяційної формули Ньютона збігатиметься з залишковим член інтерполяційної формули Лагранжа. Отже,
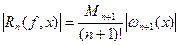 .
.
Дата публикования: 2014-11-19; Прочитано: 1318 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
