 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Інтерполяційний многочлен Лагранжа
|
|
Нехай у точках 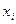 ,
, 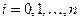 ,
, 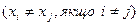 задано значення функції
задано значення функції 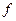 :
: 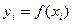 ,
, 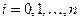 . Треба побудувати многочлен
. Треба побудувати многочлен 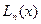 степені
степені 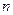 , який у вузлах
, який у вузлах 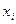 ,
, 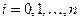 , набуває тих самих значень, що і функція
, набуває тих самих значень, що і функція 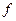 , тобто
, тобто
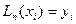 ,
, 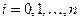 . (6)
. (6)
Інтерполяційний многочлен шукатимемо у вигляді:
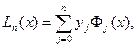 (7)
(7)
де 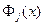 – многочлен степеня
– многочлен степеня 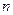 , що у вузлах інтерполяції задовольняє умови:
, що у вузлах інтерполяції задовольняє умови:
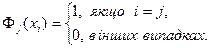
Даний варіант запису многочлена 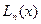 називають інтерполяційним многочленом Лагранжа. Для пошуку
називають інтерполяційним многочленом Лагранжа. Для пошуку 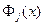 знаходять многочлен степеня
знаходять многочлен степеня 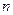 , що перетворюється в нуль у вузлах інтерполяції
, що перетворюється в нуль у вузлах інтерполяції 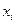 ,
, 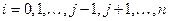 і дорівнює одиниці в точці
і дорівнює одиниці в точці 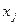 . Многочлен, що задовольняє ці вимоги, може бути записаний у вигляді:
. Многочлен, що задовольняє ці вимоги, може бути записаний у вигляді:
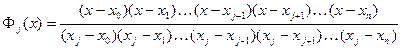 . (8)
. (8)
Підставивши вираз для 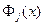 у формулу (7), дістанемо вираз інтерполяційного многочлена
у формулу (7), дістанемо вираз інтерполяційного многочлена
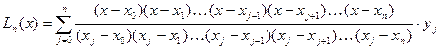 , (9)
, (9)
який називається інтерполяційним многочленом Лагранжа, а наближену рівність
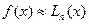 (10)
(10)
– інтерполяційною формулою Лагранжа.
Розглянемо два окремих випадки інтерполяційної формули Лагранжа (9).
10. Нехай 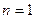 , тобто значення функції
, тобто значення функції 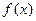 задано в двох вузлах
задано в двох вузлах 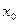 і
і 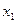 . Позначимо ці значення через
. Позначимо ці значення через 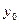 і
і 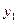 . Тоді з формули (9) дістанемо
. Тоді з формули (9) дістанемо
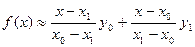 . (11)
. (11)
Формулу (11) називають формулою лінійного інтерполювання. При лінійному інтерполюванні дуга кривої 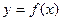 на відрізку
на відрізку 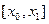 замінюється відрізком прямої (11), що лежить між точками
замінюється відрізком прямої (11), що лежить між точками 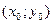 і
і 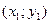 .
.
20. Нехай 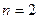 . У цьому випадку функцію
. У цьому випадку функцію 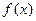 задано в трьох вузлах
задано в трьох вузлах 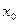 ,
, 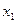 і
і 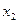 значеннями
значеннями 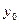 ,
, 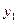 і
і 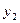 . Тоді з формули (9) дістанемо
. Тоді з формули (9) дістанемо
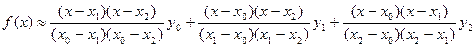 . (12)
. (12)
Формулу (12) називають формулою квадратичного інтерполювання. При квадратичному інтерполюванні дуга кривої 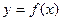 на відрізку
на відрізку 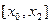 замінюється дугою параболи (12), що лежить між точками
замінюється дугою параболи (12), що лежить між точками 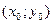 ,
, 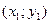 і
і 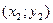 .
.
Інтерполяційний многочлен Лагранжа можна записати компактніше. Для цього введемо многочлен 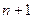 -го степеня вигляду
-го степеня вигляду
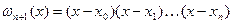 . (13)
. (13)
Виконавши диференціювання функції (13) по 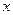 , дістанемо
, дістанемо
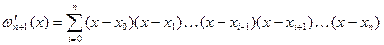 .
.
Поклавши тут 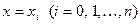 , матимемо
, матимемо
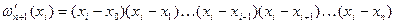 . (14)
. (14)
Підставивши (13) і (14) в (9), знайдемо
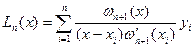 . (15)
. (15)
Вирази 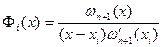 , що є коефіцієнтами при
, що є коефіцієнтами при 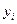
 у многочлені Лагранжа, називають коефіцієнтами Лагранжа.
у многочлені Лагранжа, називають коефіцієнтами Лагранжа.
Побудова інтерполяційного многочлена Лагранжа у такому вигляді для кожної конкретної задачі пов’язана зі значними обчислювальними затратами. Для виходу з цієї ситуації можна скористатись засобами пакету Mathcad.
Приклад 2. Для даних, наведених в прикладі 1 знайти коефіцієнти Лагранжа, побудувати відповідний многочлен Лагранжа, знайти наближене значення многочлена Лагранжа в точці 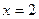 та побудувати графіки коефіцієнтів та многочлена Лагранжа.
та побудувати графіки коефіцієнтів та многочлена Лагранжа.
Розв’язання. На лістингу 2 наведено функції: 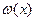 ,
, 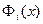 та многочлен Лагранжа
та многочлен Лагранжа 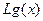 у звичайному та розгорнутому вигляді, а також графіки коефіцієнтів та многочлена.
у звичайному та розгорнутому вигляді, а також графіки коефіцієнтів та многочлена.
Для розв’язання поставленої задачі можна побудувати спеціальну процедуру-функцію 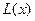 . На лістингу 3 наведено процедуру-функція
. На лістингу 3 наведено процедуру-функція 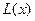 , побудовано її графік та обчислено значення многочлена в точці
, побудовано її графік та обчислено значення многочлена в точці 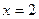 . Перевага так побудованого многочлена Лагранжа є його компактність, а недолік – неможливість із
. Перевага так побудованого многочлена Лагранжа є його компактність, а недолік – неможливість із 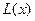 одержати звичайний многочлен.
одержати звичайний многочлен.
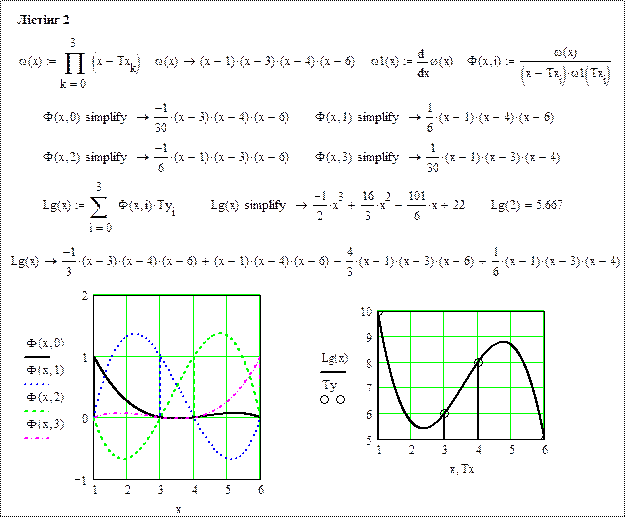
Дата публикования: 2014-11-19; Прочитано: 2812 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
