Оцінка похибки інтерполяційної формули Лагранжа

Якщо функція 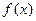на відрізку 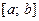є многочленом степеня, що менший або дорівнює 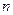, то з єдиності інтерполяційного многочлена випливає, що інтерполяційний многочлен 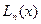тотожно дорівнює 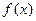, тобто при .

Якщо функція 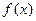на відрізку 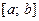, який містить вузли інтерполювання не є многочленом степеня, що менший або дорівнює 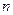, то різниця

(16)

дорівнюватиме нулю лише у вузлах інтерполювання , а в інших точках відрізка 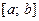вона відмінна від тотожного нуля. Функцію , яка характеризує точність наближення функції 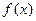інтерполяційним многочленом 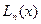, називають залишковим членом інтерполяційної формули (9), або похибкою інтерполювання. Якщо відомий аналітичний вираз функції 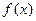, то можна оцінити . У цьому випадку справедлива така теорема.

Теорема. Якщо вузли інтерполювання різні і належать відрізку 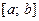, а функція 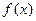диференційована 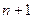раз на відрізку 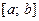, то для будь-якої точки існує така точка , що для похибки інтерполювання справедлива рівність

, (17)

де .

Якщо ввести позначення , тоді для абсолютної похибки інтерполяційної формули Лагранжа в поточній точці , дістанемо оцінку

, (18)

а на всьому відрізку :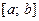

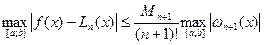. (19)

Приклад 3. Оцінити похибку наближення функції в точці і на всьому відрізку з допомогою інтерполяційного многочлена Лагранжа другого степеня, побудованого з вузлами , , .

Розв’язання. Знайдемо:

, , ,

.

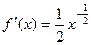На основі нерівності (18) одержимо

.

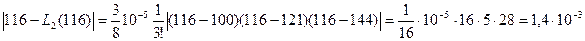Згідно з оцінкою (19)

.