Мінімізація оцінки похибки інтерполяції. Многочлени Чебишева

З формули (18) видно, що абсолютна похибка інтерполяційної формули Лагранжа пропорційна добутку двох множників 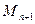і , з яких 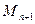залежить лише від функції 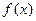, а величина другого, , визначається виключно вибором вузлів інтерполювання. Зменшити величину абсолютну похибку інтерполяційної формули Лагранжа можна таким вибором вузлів інтерполювання, за якого множник набуває найменшого максимального значення на відрізку 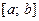. Одним із способів мінімізації множника є використання многочленів Чебишева.

Для простоти спочатку розглянемо випадок стандартного відрізка .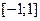

Многочлени Чебишева. Многочлени Чебишева 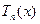, 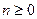на відрізку 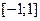визначаються формулою

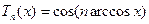. (20)

При маємо: .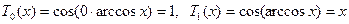

Далі із тотожності

або

,

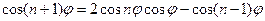при 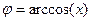, одержимо

(21)

Покладаючи в (21) 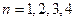т.д., знаходимо:

Графіки виписаних поліномів Чебишева наведено на рис. 1.

Якщо розглядуваний відрізок 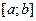відмінний від стандартного, то його завжди можна привести до стандартного заміною змінної

.

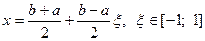Чебишев довів, що величина 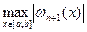має найменше значення, якщо вузлами інтерполювання є числа 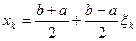, де 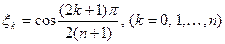– нулі многочлена Чебишева 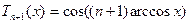. Вони дійсні різні, належать інтервалу 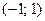і згущаються біля кінців інтервалу.

Доведено, що за такого вибору вузлів інтерполювання

,

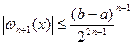а оцінка (18) має вигляд

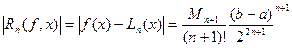, (220)