Нормальный закон распределения. Нормальным законом распределения вероятностей называется такое распределение вероятностей непрерывной случайной величины

Нормальным законом распределения вероятностей называется такое распределение вероятностей непрерывной случайной величины, у которой плотность распределения имеет вид

,

где 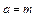— математическое ожидание;

— среднее квадратичное отклонение.

Функция 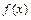удовлетворяет требованиям к плотности распределения:

1) ;

2) .

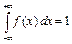График дифференциальной функции называют нормальной кривой (кривой Гаусса) и имеет вид, симметричный относительно прямой , а ось абсцисс является горизонтальной асимптотой кривой.

Если принять , то:

— функция Гаусса;

— локальная функция Лапласа;

тогда

,

где — нормированная переменная.

— табличная функция Лапласа.

Функция распределения нормального закона имеет вид:

.

а) Вероятность не превышения заданного значения х:

;

.

б) Вероятность превышения заданного значения х:

;

.

в) Вероятность попадания значения случайной величины в заданный интервал:

,

где

; .

Вероятность того, что Х примет значение, которые принадлежит интервалу вычисляется по формуле:

,

где — функция Лапласа.

Вероятность того, что абсолютная величина отклонения случайной величины Х от своего математического ожидания а меньше положительного числа :

.

В частности, если , то:

.

Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:

.

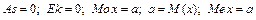Случайные величины, которые распределены по нормальному закону распределения, широко распространенные в природе. Такими случайными величинами могут быть рост человека, вес пойманной рыбы, дальность полета снаряда при стрельбе с какого-то одного вида орудия и т.д.

Пример 1. Случайная величина х распределена по нормальному закону с параметрами а = 6,5 и 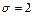. Вычислить вероятность того, что:

а) значение случайной величины попадет в интервал

б) отклонение значения от среднего не превысит 4.